Um tanque de diâmetro 10 m está inicialmente preenchido com água acima do centro de uma válvula de diâmetro próxima ao fundo. A superfície do tanque está aberta para a atmosfera, e o tanque drena a água por um tubo de comprimento conectado à válvula. O coeficiente de atrito do tubo é dado como , e a velocidade de descarga é expressa como , onde é a altura da água acima do centro da válvula. Determine (a) a velocidade de descarga inicial do tanque e (b) o tempo necessário para esvaziar o tanque. O tanque pode ser considerado vazio quando o nível de água baixa para o centro da válvula.
Passo 1
Para evitar confusões durante a questão vamos usar o símbolo para volume, para vazão volumétrica, e o símbolo para expressar velocidade escalar ou vetorial.
Abaixo temos um esquema do tanque.
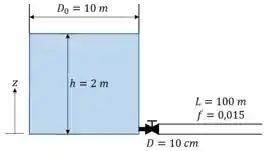
No instante inicial a altura é igual a dois metros. Aplicando isto à fórmula podemos calcular a velocidade :
Passo 2
A vazão do tanque é dada pela área da válvula vezes a velocidade
A quantidade de volume que deixou um tanque é igual a vazão vezes o tempo. Para uma variação de tempo infinitesimal temos:
Essa equação por si só não resolve nosso problema, pois não sabemos o comportamento da variável . Então, vamos procurar uma outra maneira de expressão o volume que sai do tanque
Passo 3
Existe uma outra forma de calcular o volume que sai do tanque. Veja a imagem abaixo, onde uma certa quantidade de volume saiu do tanque (azul escuro).
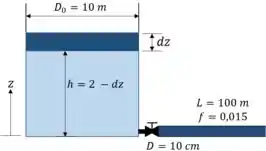
A quantidade de volume que saiu do tanque é:
Passo 4
Vamos igualar as duas expressões para o volume que sai do tanque:
Simplificando:
Como queremos encontrar o tempo, vamos isolar e reorganizar a equação:
Aplicando os valores:
E agora integramos! O tempo inicia em zero e vai até o valor que queremos descobrir. O varia entre e