Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 3.Problemas - Ex. 68

Um tanque com volume de 400   m ³ está sendo construído para armazenar gás natural liquefeito, que pode ser considerando essencialmente como metano puro. Se o tanque deve conter 90 % de líquido e 10 % de vapor, em volume, a 100   k P a , qual será a massa (em kg) de gás armazenado no tanque. Qual será o título da mistura líquido-vapor no tanque?

Passo 1

E aí, galerinha! Tudo tranks? Vamos lá resolver nosso probleminha!

Para o metano, temos a seguinte tabela de saturação...

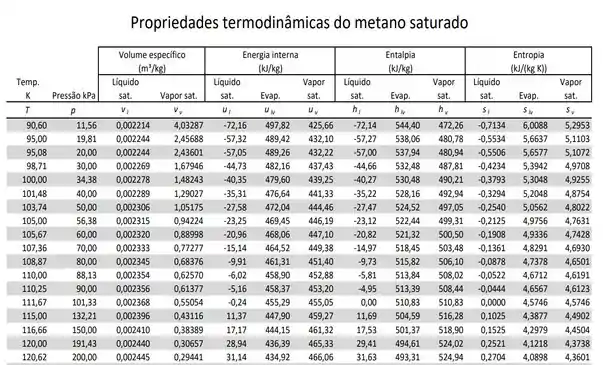
Por interpolação, vamos calcular v f e v g em 100   k P a

100 - 90 v f - 0,002356 = 101,33 - 100 0,002368 - v f

1,33 v f - 1,33 ⋅ 0,002356 = 0,0 2368 - 10 v f

v f = 0,00236

100 - 90 v g - 0,61377 = 101,33 - 100 0,55054 - v g

v g = 0 , 5726

Passo 2

Obtido v g e v f , pra achar a massa líquida e vapo, vamos usar a fórmula abaixo...

m l í q = V l í q v f

m v a p = V v a p v g

Daí, como nosso tanque de 400   m ³ é 90 % de líquido e 10 % de vapor...

m l í q = 400 ⋅ 0,9 0,00236 = 152542   k g

m v a p = 400 ⋅ 0,1 0 , 5726 = 69,9   k g

Podemos obter a massa total somando isso...

m t o t a l = m l í q + m v a p

m t o t a l = 152542   k g + 69,9   k g

m t o t a l = 152612   k g

E o título da mistura líquido-vapor no tanque...

x = m v a p m t o t a l

x = 69,9 152612

x = 4,58 ⋅ 10 - 4

Pronto! Missão cumprida!

Resposta

m t o t a l = 152612   k g

x = 4,58 ⋅ 10 - 4

Exercícios de Livros Relacionados

Deduza a equação 2-38.
a) Mostre que as constantes críticas de uma substância obedecem à equação de Dieterici de estado, P v - be a v R T = R T , são P C = a 4 e 2 b 2 ,v C = 2 b ,T C = a 4 R b b) Compare a razão P C v C /
a) Usando a relação cíclica Eq. (2-41), encontre o coeficiente de dilatação β de uma substância que obedece à equação de Dieterici de estado, dada no problema 2.30.b) A altas temperaturas e grandes vo
Usando as constantes críticas encontradas na T a b e l a2.3 , calcule o valor de b na equação de van der Waals para o C O 2 (a) a partir de v c e (b) a partir de T c e P c .