Em todos os chamados gases diatômicos, algumas das moléculas estão dissociadas em átomos separados, a fração dissociada aumentando com a temperatura. O gás como um todo consiste, então, em uma porção diatômica e outra monoatômica. Muito embora cada componente possa atuar como um gás ideal, a mistura não o e, porque o número de moles varia com a temperatura. O grau de dissociação de um gás diatômico e definido como a razao da massa
, da porção monoatômica para a massa total do sistema.
(a) Mostre que a equação de estado do das é
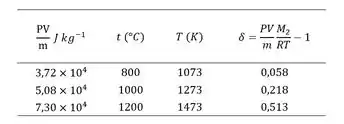
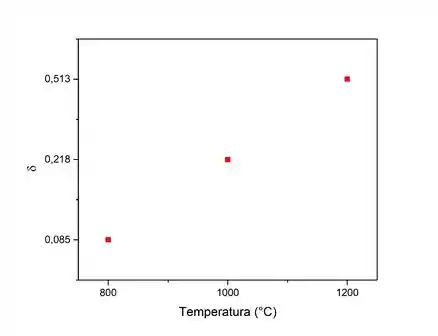
Onde é o “peso” molecular da componente diatômica. Suponha que o gás obedece à lei de Dalton. (b) A tabela abaixo dá uma lista de valores medidos da razão para vapor iodado a três temperaturas diferentes. Calcule e mostre, em um gráfico o grau de dissociação como função de temperatura.

Passo 1
(a) De acordo à lei de Dalton das pressões parciais, a pressão total de uma mistura de gás é:
Onde é a pressão parcial da componente monoatômica e a componente parcial da componente diatômica, definidas de acordo a equação dos gases ideais como:
Substituindo em
Por definição, é a massa da componente diatômica sobre a massa molar :
é a massa da componente monoatômica sobre a massa molar da dissociação da componente diatômica .
Substituindo em , temos:
Substituindo
Lembrando que , nossa demonstração está feita:
Passo 2
(b) Da equação demostrada no passo anterior, temos que:
O peso molecular do vapor iodado é e é .
Resposta
Resposta nos passos