O tubo em forma de U, na Figura 2.18, de 1 cm2 de seção reta uniforme, contem mercúrio até a altura mostrada. A pressão barométrica é de 750 Torr. O lado esquerdo do tubo está agora fechado no topo, e o lado direito está conectado a uma boa bomba de vácuo. (a) Quanto é o nível do mercúrio desce no lado esquerdo e (b) qual é a pressão final do ar encerrado? A temperatura permanece constante.
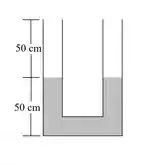
Passo 1
(a) Opa, beleza???
Para resolver nosso problema primeiro vamos lembrar os dados que temos com suas respetivas conversões:
Se assumimos que a pressão na parte do tubo onde está o ar começa em e vai até (Onde é a pressão do lado esquerdo) podemos fazer:
O anterior, porque Assim, temos então:
A pressão no braço direito é:
Então eu sei que o mercúrio se moverá centímetros de um lado (para baixo) e do outro (para cima). Portanto, a distância total que o mercúrio se move é de .
Usando a lei de Pascal:
Fazendo agora:
Temos então uma equação quadrática da forma:
Com soluções:
Onde a solução positiva é a que se toma como real:
Passo 2
(b) Calculando a pressão final do ar encerrado:
Resposta
a)
b)