Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 5.Problemas - Ex. 91
Uma unidade de troca de calor com água gelada é projetada para esfriar 5 m³/s de ar inicialmente a 100 kPa e 30 °C até 100 kPa e 18 °C, usando água a 8 °C. Determine a temperatura máxima de saída da água, considerando a vazão mássica da água equivalente a
2 kg/s.
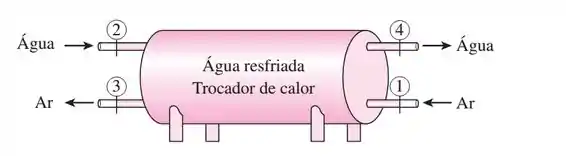
Passo 1
O primeiro passo é saber que trocadores de calor tipicamente não envilvem interações de trabalho e possuem variação de energia cinética desprezíveis para cada fuido corrente.
Aplicando o balanço de massa para o trocador de calor do sistema, obtemos a equação:
Aqui, os fluxos mássico de entrada e saída são e respectivamente
Aplicando o balanço de massa para o trocador e calor, obtemos a equação:
As taxas de energia líquida de entrada e de saída são respectivamente e respectivamente, ao fluxo de calor é e as entalpias de entrada e de saída são e respectivamente
Passo 2
Considerando o fluxo mássico do ar:
Em que a densidade do ar é e a vazão volumétrica do ar é
Consideranto a equação dos gases ideais:
Assumindo a constante dos gases para o ar como:
e a temperatura de entrada é
Substituindo:
Substituindo , na equação (1):
Passo 3
Calculando a temperatura média do ar:
Em que temperatura de saída é
Substituindo ,
Para a temperatura , considerando as propriedades dos gases ideais e calculando o calor específico a pressão constante utilizando a interpolação:
Considerando a taxa de transferência na corrente de ar:
)
Substituindo , e 30ºC e
Passo 4
O calor perdido pela corrente de ar é igual ao calor ganhado peloa corrente de água:
Em que o fluxo maxico de água é
Substituindo por , e
Portanto, a temperatura de saída é de