Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 5.Problemas - Ex. 34

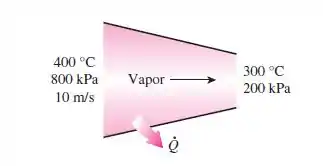
Vapor entra em um bocal a 400   ° C e 800   k P a com uma velocidade de 10   m / s e sai a 300   ° C e 200   k P a , enquanto perde calor a uma taxa de 25   k W . Para uma area de entrada de 800   c m 2 , determine a velocidade e a vazão volumétrica do vapor na saída do bocal.

Passo 1

Precisamos determinara velocidade e vazão ou fluxo volumétrico de saída.

Perceba que este é um processo em regime permanente, pois não há mudança com o tempo.

Energia potencial não é considerada e não há interação de trabalho.

Por ser um sistema de controle de volume e regime permanente podemos escrever o balanço de energia da seguinte forma:

E ˙ i n - E ˙ o u t = Δ E ˙ s i s t e m a

Devido não possuir variação interna, energia cinética e potencial. Exceto pela entalpia possuir neste caso variação, logo ela entra no balanço final:

Δ E ˙ s i s t e m a = 0

Logo temos:

E ˙ i n - E ˙ o u t = 0

E ˙ i n = E ˙ o u t

m ˙ ∙ h 1 + V 1 2 2 = m ˙ ∙ h 2 + V 2 2 2 + Q o u t

Isolando V 2 :

V 2 = V 1 2 + 2 ∙ h 1 - Q o u t   ∙ 2 m ˙ - ( h 2 ∙ 2 )

Certo, possuímos a equação que determinara a velocidade final, mas para isso precisaremos olhar as tabelas do livro para determinarmos h 1 e h 2 e seus volumes específicos sobre as condições de temperatura e pressão de entrada e saída.

Passo 2

Dados retirados da tabela(A-6) do livro

Condições de entrada:

P 1 = 800   k P a

T 1 = 400 ° C

Temos: h 1 = 3267,7   k J / k g e v 1 = 0,38429   m 3 / k g

Condições de saída:

P 2 = 200 k P a

T 2 = 300   ° C

Temos: h 2 = 3072,1   k J / k g   e v 2 = 1,31623   m 3 / k g

Possuindo os dados necessários vamos determinar o fluxo de massa para encontrar a velocidade da saída:

m ˙ = V A v

m ˙ = V 1 A 1 v 1

m ˙ = 10 ∙ 0,008 0,38429

m ˙ = 2,082   k g / s

Agora que possuímos o fluxo de massa, vamos substituir na primeira equação que deduzimos:

V 2 = V 1 2 + 2 ∙ h 1 - Q o u t   ∙ 2 m ˙ - ( h 2 ∙ 2 )

V 2 = 10 2 + 2 ∙ 3267,7   k - 25   k ∙ 2 2,082 - ( 3072,1   k ∙ 2 )

V 2 = 605,87   m / s

Passo 3

Determinado o fluxo volumétrico de saída:

Como o fluxo de massa é o mesmo para entrada e saída ao multiplicarmos pelo volume específico encontraremos o fluxo de volumétrico, aplicando:

V ˙ 2 = m ˙ ∙ v 2

V ˙ 2 = 2,082 ∙ 1,31623

V ˙ 2 = 2,74   m 3 / s

Resposta

V 2 = 605,87   m / s

V ˙ 2 = 2,74   m 3 / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ar escoa isentropicamente por um duto de área variável. Na seção 1, A 1 = 20c m 2 ,p 1 = 300k P a ,ρ 1 = 1,75 k g m 3 ,eM a 1 = 0,25 . Na seção 2, a área é exatamente a mesma, mas o escoamento é bem m
Ar, nas condições de estagnação de 500 K e 200 kPa, escoa por um bocal. Na seção 1, em que a área é 12 cm2, a massa específica é 0,32 kg/m3. Admitindo escoamento isentrópico, (a) determine a vazão em
Uma força F = 1.100 N empurra um pistão de 12 cm de diâmetro através de um cilindro isolado contendo ar a 20oC, como na Figura P9.48. O diâmetro de saída é 3 mm e pa 5 1 atm. Calcule (a) Vs, (b) Vp e
Considere o bocal Venturi da Figura 6.40c, com D = 5 cm e d = 3 cm. A temperatura de estagnação é de 300 K e a velocidade a montante é V1 = 72 m/s. Se a pressão na garganta é de 124 kPa, calcule, pela
Ar escoa de um reservatório a 20oC e 500 kPa por um duto e forma um choque normal a jusante de uma garganta de 10 cm2 de área. Por uma casual coincidência, verifica-se que a pressão de estagnação a ju