Potência Elétrica e Expansão Não Resistida
Produzido por Philip Canabarro BlockerTeoria
Como podemos calcular a potência elétrica ?
Anteriormente, nós descobrimos que a transferência de energia elétrica pode ser considerada trabalho, porque o movimento dos elétrons é causado por uma força. Ou seja, essa troca de energia só acontece por causa da força elétrica.
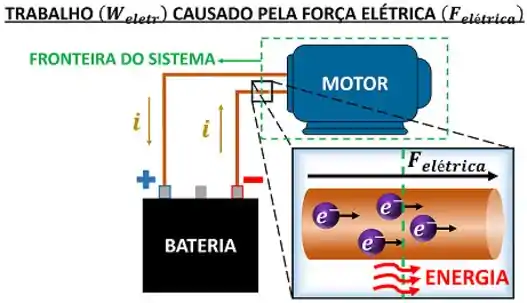
Em outras palavras, a gente passou a entender que o deslocamento de elétrons para dentro e para fora de um sistema é considerado trabalho. No entanto, ainda resta uma dúvida: como podemos calcular a taxa de transferência de energia causada pelo trabalho elétrico? Refazendo a pergunta: como podemos calcular a potência elétrica ?

Fórmula da potência elétrica
Então vamos responder essa pergunta com o exemplo ilustrado pela figura abaixo. Imagine um sistema formado por um motor elétrico, um eixo girando e um tanque rígido contendo um gás. O motor elétrico é alimentado por uma corrente elétrica de com uma diferença de potencial de . Qual é a taxa de trabalho que o sistema recebe?
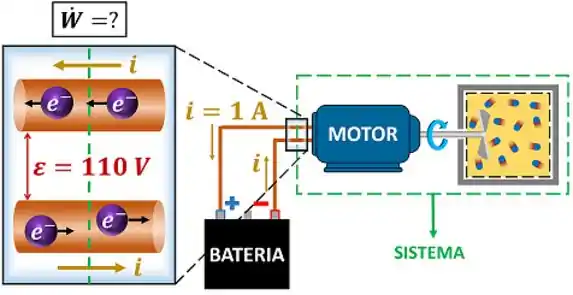
A fórmula para calcular essa taxa de trabalho é:
onde:
- é a taxa de trabalho elétrico. Essa variável também é chamada de potência elétrica. Ela é medida em watt de acordo com o Sistema Internacional (S.I.);
- é a diferença de potencial elétrico entre a corrente elétrica que está entrando e a corrente elétrica que está saindo. Ela é medida em volt de acordo com o S.I.;
- é a corrente elétrica que entra no sistema. Ela é medida em ampère de acordo com o S.I.
Sabendo dessa equação, o resultado vale:
O sinal negativo indica que o sistema recebe energia. Isso quer dizer que a vizinhança do sistema (bateria) realiza trabalho sobre o sistema (motor, eixo e tanque com gás).
Em todo tipo de trabalho existe uma força vencendo uma resistência
Em todos os tipos de trabalho que estudamos até agora, existia um deslocamento causado por uma força. No trabalho elétrico, o deslocamento dos elétrons é causado pela força elétrica. No trabalho de movimento de fronteira, o deslocamento do pistão é causado pela força da pressão. Por fim, no trabalho de eixo, o giro do eixo também é causado por uma força.
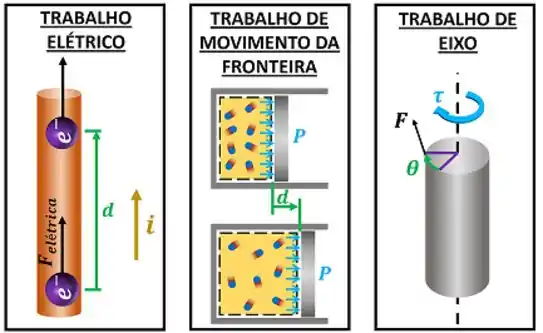
Se não tivesse uma força empurrando um bloco imóvel, ele ficaria parado por conta da inércia. Se não existisse a força da pressão, o pistão continuaria parado pelo mesmo motivo. Sem uma força empurrando os elétrons, eles ficariam parados por causa da resistência elétrica. Ou seja, sem uma força para vencer essas resistências, não existiria deslocamento nem trabalho!
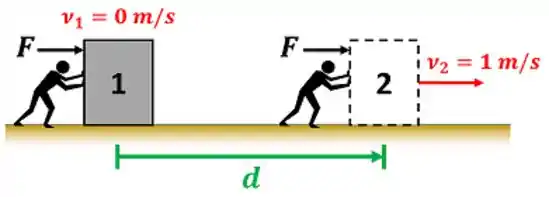
Dizendo isso de outra forma, é necessário que o bloco e o pistão ganhem energia através do trabalho para eles vencerem a resistência da inércia! Também é necessário que o elétron ganhe energia por trabalho para ele vencer a resistência elétrica.
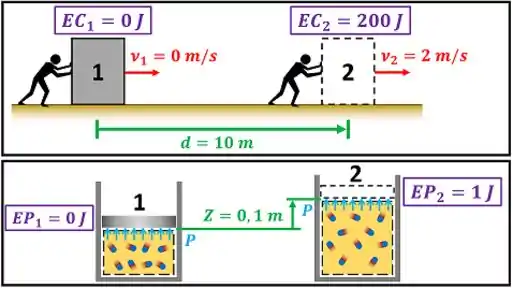
Todo tipo de trabalho que vimos até agora estava ligado a algum tipo de resistência ao movimento. Isso quer dizer que só existe trabalho, quando existe resistência ao deslocamento? Vamos responder essa pergunta com um exemplo!
Toda expansão de sistema é trabalho?
Para responder a dúvida de cima, vamos pensar em um exemplo muito parecido com o trabalho de movimento de fronteira de um sistema. No trabalho de movimento de fronteira, o volume do sistema aumenta, porque ele empurra um pistão com a força da sua pressão. No exemplo que a gente vai estudar, não tem resistência para o gás aumentar de volume!
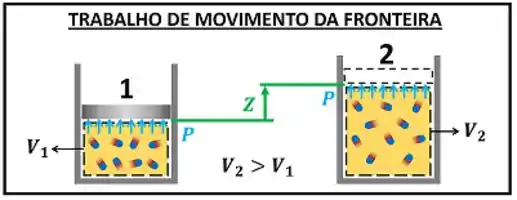
Nesse exemplo, vamos imaginar um tanque dividido em duas regiões por uma membrana. Uma parte tem um gás e a outra não tem nenhuma substância. Imagine que essa membrana se rompa e o gás comece a vazar para o outro lado. Com isso, o gás começa a expandir, porque sua fronteira se movimenta.
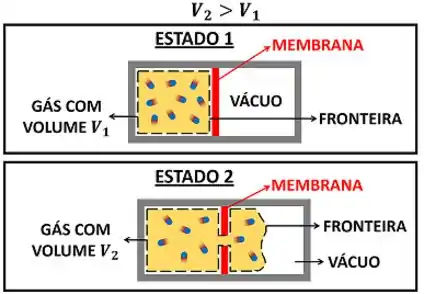
Se o gás não tem pistão para empurrar, nem resistência da inércia para vencer, ele está realizando trabalho de fronteira? Essa pergunta é importante! Se a resposta para ela for sim, então existe trabalho sem resistência ao deslocamento!
A diferença entre a expansão não resistida e o trabalho de movimento de fronteira
Para responder a pergunta de cima, é melhor refazê-la. Existe trabalho, quando o gás não precisa ganhar energia para movimentar a sua fronteira?
Não, porque o trabalho é um tipo de transferência de energia! Se o sistema não precisa dar nem receber energia para expandir, ele não transfere energia nem realiza trabalho!
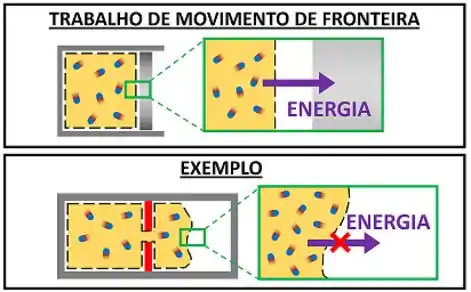
Isso significa que esse processo de vazamento de gás não é trabalho! Ele não pode ser chamado de trabalho de expansão do sistema ou trabalho de movimento de fronteira. Ele é chamado de expansão não resistida. Esse nome ajuda a lembrar que não existe resistência ao movimento do gás nesse processo. Por conta disso, ele não precisa dar energia para se mover!

No trabalho de movimento de fronteira, o sistema precisa dar energia ao pistão para ele vencer a resistência da inércia e se mover! O sistema precisa realizar trabalho sobre o pistão para ele se deslocar e o sistema conseguir expandir sua fronteira.
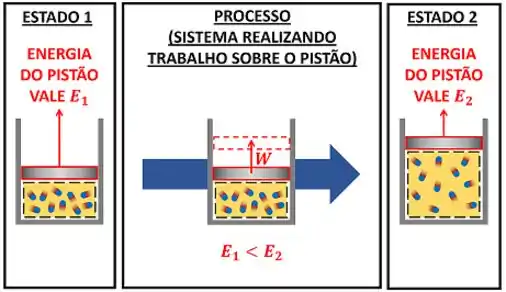
Esse exemplo mostra que para existir trabalho, precisa existir resistência ao movimento! Se não existir resistência, o sistema não ganha nem perde energia. Se não existe transferência de energia, o processo não pode ser chamado de trabalho!
Fórmula da potência elétrica W ˙ e l e t r
Em todo tipo de trabalho existe uma força vencendo uma resistência
Toda expansão de sistema é trabalho?
A diferença entre a expansão não resistida e o trabalho de movimento de fronteira
Exercícios Resolvidos
Exercício Resolvido #1
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 96-4.89
Uma bateria de acumuladores, bem isolada termicamente, está sendo carregada. A tensão de carga é e a corrente igual a . Considerando a bateria como o sistema, determine o trabalho realizado num período de horas.
Passo 1
Fala, minha gente! Prontos para exercitar a teoria com essa questão de potência elétrica?
O enunciado quer saber quanto vale o trabalho elétrico total que a bateria recebe ao ser carregada por . A figura abaixo mostra os dados que temos para fazer esse cálculo.
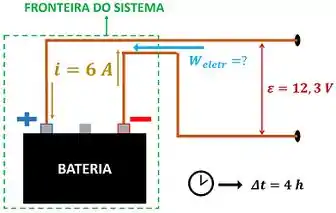
é a diferença de potencial elétrico da bateria, é a corrente elétrica que pela bateria e é a duração do carregamento da bateria.
Queremos calcular o trabalho elétrico que a bateria recebe, mas sabemos apenas calcular a potência que a bateria recebe através da equação abaixo!
Isso quer dizer que primeiro, calcularemos a potência elétrica que a bateria recebe e depois entenderemos como converter essa potência elétrica no trabalho elétrico que a questão quer!
Passo 2
Então vamos começar calculando o valor de ! Fazemos isso através da equação presente no passo 1!
Agora que temos esse valor, somos capazes de calcular .
Passo 3
Para fazer a conversão de pra , temos que entender o que significa. é o trabalho que a bateria recebe a cada segundo de carregamento. Ou seja, pra saber quanto vale o trabalho total que ela recebe, temos que multiplicar o trabalho que ela recebe a cada segundo pela quantidade de segundos que a bateria é carregada.
No entanto, o valor que o enunciado nos deu está em horas, não segundos! Convertemos esse tempo de horas pra segundo, multiplicando por !
Substituindo esse valor na fórmula de trabalho que deduzimos, encontramos:
Aeeeee! Achamos o trabalho que o enunciado pediu!!! Show!
Resposta
Exercício Resolvido #2
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 96-4.90
Uma resistência elétrica de é alimentada com uma corrente de . Determine a potência dissipada na resistência.
Passo 1
Oi, galera bonita! Vamos exercitar a teoria com essa questão de potência elétrica?
O enunciado quer saber quanto vale a potência elétrica que a resistência elétrica de dissipa. A figura abaixo mostra os dados que temos para fazer esse cálculo.
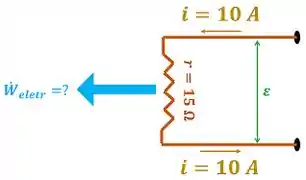
é a diferença de potencial elétrico da resistência, é a corrente elétrica que passa pela resistência e é o valor da resistência elétrica.
Queremos calcular a potência que nosso sistema (a bresistência) PERDE, mas só conhecemos a abaixo equação que calcula a potência elétrica que um sistema GANHA.
Pra piorar nossa situação, não possuímos o valor da diferença de potencial que aparece na equação. Isso quer dizer que temos dois problemas pra resolver pra conseguir fazer a questão. Primeiro, temos que achar quanto vale . Depois, temos que adaptar a equação que calcula a potência que um sistema GANHA para calcular a potência que o sistema PERDE.
Passo 2
Então vamos começar calculando o valor de ! Fazemos isso através da lei de Ohm! Essa lei diz que a diferença de potencial é igual a resistência do circuito multiplicada pela corrente que passa pelo circuito. Logo:
Substituindo os dados que temos:
Agora que temos esse valor, somos capazes de calcular .
Passo 3
Para adaptar a equação da potência , vamos dividir o cálculo de em duas etapas. Primeiro, vamos calcular o valor dessa potência elétrica sem o seu sinal. Depois vamos determinar qual é o sinal de .
Achamos o valor de sem o sinal, usando a equação do passo 1 sem o sinal de menos.
Agora, temos que determinar qual é o sinal dessa potência . Fazemos isso, lembrando da regra de sinal que usamos para a potência. Se o sistema recebe potência , o sinal da potência é negativo e devemos colocar um sinal de menos na frente de .
Se o sistema perde potência , o sinal da potência é positivo.
Como no caso da resistência, a potência está sendo perdida (dissipada), o sinal de é positivo. Logo, o valor de permanece do jeito que calculamos antes!
Resposta
Exercício Resolvido #3
Elaboração própria
Uma bateria de alimenta por um circuito elétrico que possui uma resistência elétrica de . Considerando a bateria como um sistema termodinâmico, determine o trabalho elétrico realizado pela bateria sobre o circuito.
Passo 1
E aí, pessoal! Prontos para exercitar a teoria com essa questão de potência elétrica?
O enunciado quer saber quanto vale o trabalho elétrico total realizado pela bateria. A figura abaixo mostra os dados que temos para fazer esse cálculo.
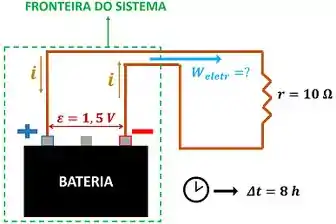
é a diferença de potencial elétrico da bateria, é a corrente elétrica que passa pelo circuito e é a resistência elétrica do circuito.
Queremos calcular o trabalho que nosso sistema (a bateria) FORNECE mas só conhecemos a abaixo equação que calcula a potência elétrica que um sistema RECEBE.
Pra piorar nossa situação, não possuímos o valor da corrente que aparece na equação.
Isso quer dizer que temos três problemas pra resolver pra conseguir fazer a questão.

- Temos que achar o valor de .
- Temos que adaptar a equação que calcula a potência que um sistema GANHA para calcular a potência que o sistema DÁ.
- Por fim, temos que converter essa potência elétrica no trabalho elétrico que a questão quer!
Passo 2
Então vamos começar calculando o valor de ! Fazemos isso através da lei de Ohm! Essa lei diz que a diferença de potencial é igual a resistência do circuito multiplicada pela corrente que passa pelo circuito. Logo:
Reorganizando essa equação, achamos uma fórmula pra .
Substituindo os dados que temos:
Agora que temos esse valor, somos capazes de calcular .
Passo 3
Para adaptar a equação da potência , vamos dividir o cálculo de em duas etapas. Primeiro, vamos calcular o valor dessa potência elétrica sem o seu sinal. Depois vamos determinar qual é o sinal de .
Achamos o valor de sem o sinal, usando a equação do passo 1 sem o sinal de menos.
Agora, temos que determinar qual é o sinal dessa potência . Fazemos isso, lembrando da regra de sinal que usamos para trabalho e potência. Se o sistema recebe potência , o sinal da potência é negativo e devemos colocar um sinal de menos na frente de .
Se o sistema fornece potência (isso é a mesma coisa que dizer que o sistema perde potência), o sinal da potência é positivo.
Como no caso da bateria, a potência está sendo fornecida, o sinal de é positivo. Logo, o valor de permanece do jeito que calculamos antes!
Então vamos partir pro cálculo do trabalho elétrico !
Passo 4
Para fazer a conversão de pra , temos que entender o que significa. é o trabalho que a bateria recebe a cada segundo de carregamento. Ou seja, pra saber quanto vale o trabalho total que ela recebe, temos que multiplicar o trabalho que ela recebe a cada segundo pela quantidade de segundos que a bateria é carregada.
No entanto, o valor que o enunciado nos deu está em horas, não segundos! Convertemos esse tempo de horas pra segundo, multiplicando por !
Substituindo esse valor na fórmula de trabalho que deduzimos, encontramos:
Aeeeee! Achamos o trabalho que o enunciado pediu!!! Show!
Resposta
Exercício Resolvido #4
Elaboração própria
Uma pessoa estava com muita pressa e, para degelar sua geladeira de forma mais rápida, usou o secador de cabelo de . A resistência elétrica do secador de cabelo possui . Essa resistência deve dissipar um total de de calor para derreter todo o gelo da geladeira. Considerando que a geladeira demora para degelar sozinha, calcule a quantidade de tempo que a pessoa economizou utilizando o secador de cabelo.
Passo 1
Oier, pessoas! Bora exercitar o nosso conhecimento com essa questão de potência elétrica?
O enunciado quer saber a diferença de tempo entre um degelo de geladeira usando um secador (que demora ) e um degelo normal (que demora ).
nós já conhecemos, porque a questão informou que vale . Já pode ser calculado, considerando que toda a energia dissipada pela resistência é absorvida pelo gelo. Além disso, pra achar , temos que lembrar que a potência elétrica do secador é igual ao trabalho elétrico realizado por ele dividido pelo tempo de realização do trabalho.
A figura abaixo mostra os dados que temos pra calcular .
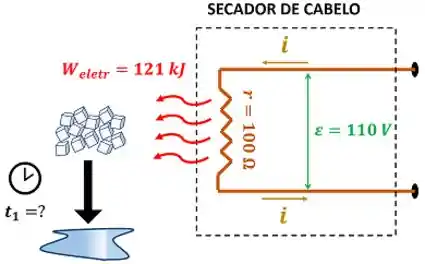
é a diferença de potencial elétrico da bateria, é a corrente elétrica que passa pelo circuito, é a resistência elétrica do circuito e é a energia dissipada pela resistência do secador.
Com todos esses dados em mãos, podemos partir para o próximo passo.
Passo 2
Vemos através da equação de , que temos que achar o valor da potência elétrica dissipaga pra calcular , No entanto, para achar , temos que encontrar o valor da corrente . Fazemos isso através da lei de Ohm! Essa lei diz que a diferença de potencial é igual a resistência do circuito multiplicada pela corrente que passa pelo circuito. Logo:
Reorganizando essa equação, achamos uma fórmula pra .
Substituindo os dados que temos:
Agora que temos esse valor, somos capazes de calcular .
Passo 3
Achamos o valor de , usando a equação abaixo.
Agora, temos que determinar qual é o sinal dessa potência . Fazemos isso, lembrando da regra de sinal que usamos para trabalho e potência. Se o sistema recebe potência , o sinal da potência é negativo e devemos colocar um sinal de menos na frente de .
Se o sistema fornece potência (isso é a mesma coisa que dizer que o sistema perde potência), o sinal da potência é positivo.
Como no caso da resistência do secador, a potência está sendo dissipada (perdida), o sinal de é positivo. Logo, o valor de permanece do jeito que calculamos antes!
Então vamos partir pro cálculo do trabalho elétrico !
Passo 4
Para calcular , precisamos primeiro converter a energia dissipada pelo secador de pra , multiplicando ela por .
Substituindo esse valor na fórmula de , achamos:
Agora, para calcular o tempo que a pessoa economizou usando o secador, temos que converter de horas pra segundos, multiplicando esse intervalo de tempo por .
Aplicando esse valor na fórmula de , achamos:
Acabooooooou! Mais um exercício pra conta! Pode comemorar! :)
Resposta
Exercício Resolvido #5
Elaboração própria
O conjunto cilindro-pistão mostrado na figura abaixo possui um membrana em seu interior. Essa membrana separa a parte interna do cilindro em duas partes. Uma parte com de volume contém um gás perfeito a e um gás perfeito. A outra parte com de volume está em vácuo absoluto. A membrana é rompida, fazendo o gás se expandir isotermicamente no cilindro. Ao fim dessa expansão, os pinos que travam o pistão são removidos, permitindo que o gás aumente isobaricamente seu volume em . Determine o trabalho total exercido pelo gás ao longo dessas duas expansões.
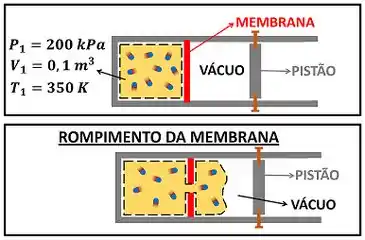
Passo 1
Oi, gente boa! Como está a vida?

Vamos exercitar os conhecimentos téoricos, fazendo uma questão de expansão não resistida?
A questão quer que a gente calcule o trabalho total relacionado a dois processos de expansão que o gás sofre. A primeira expansão faz o gás ir do estado 1 pro 2, realizando um trabalho . No segundo processo, o gás vai do estado 2 pro 3, realizando um trabalho .
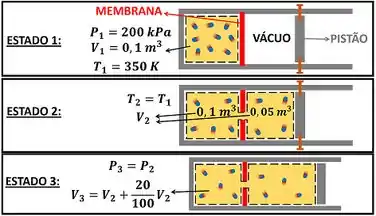
O trabalho total é justamente a soma desses dois trabalhos que o gás realiza ao se expandir.
No primeiro processo, a membrana se rompe e faz o gás se expandir com temperatura constante do estado 1 pro estado 2. No segundo processo, o gás empurra o pistão e se expande a pressão constante do estado 2 pro estado 3.
Com todas essas informações em mãos, vamos começar a questão tentando calcular .
Passo 2
Quando a membrana se rompe, o gás tende a se expandir e ocupar o volume de que antes era apenas vácuo! Dessa forma, seu volume que antes valia cresce e passa a valer .
Como o gás aumenta de volume e sua fronteira se expande, tendemos a achar que podemos calular o trabalho pela fórmula que calcula o trabalho de fronteira abaixo.
No entanto, usar essa fórmula é um erro, porque essa expansão devida ao rompimento da membrana é uma expansão não resistida. Nesse caso, o gás não precisa vencer uma resistência para se expandir e ocupar o volume que estava em vácuo! Logo, o gás não precisa gastar energia e realizar trabalho para se mover. Ou seja, o trabalho que ele realiza vale !
Pronto! Achamos o trabalho do primeiro processo de expansão. Resta apenas conhecer o valor de para achar e acabar com a questão!
Passo 3
O segundo processo de expansão é o processo do gás empurrando um pistão para se expandir. Ou seja, nesse caso, o gás precisa gastar energia para vencer a força contrária que o pistão faz. Logo, esse segundo processo se trata de um processo de trabalho de movimento de fronteira. Como ele é um processo isobárico, podemos usar a equação abaixo.
Já sabemos o valor de . Precisamos achar e . é calculado, lembrando que o volume do gás aumenta em nesse segundo processo de expansão.
Com esse dado, já poderemos calcular e na próxima etapa!
Passo 4
Achamos a partir de . Pra isso, lembramos que o primeiro processo de expansão era a temperatura constante. Logo . Usando a fórmula de gases perfeitos Pevetê Povotó, achamos:
Cortando e dos dois lados da equação:
Reorganizando a equação:
Substituindo na equação de :
Substituindo na equação de :
Aí siiiiiimmmm! Mais um exercício resolvido! Bora aproveitar o pique pra fazer mais um?
Resposta
Exercício Resolvido #6
Elaboração própria
Para refrescar seus estudos em dias de verão, um estudante teve a bilhante ideia de acionar seu pequeno ventilador com uma bateria de . A bateria gera uma corrente elétrica de através do ventilador. Nessas condições, o ventilador consegue movimentar de ar que estava para a cada segundo. Determine a velocidade desse vento que o ventilador produz.
Passo 1
E aí, pessoas lindas! Estudando muito? Então vamos aproveitar esse ânimo pra fazer um exercício de potência elétrica!

A questão quer que a gente calcule a velocidade que o vento do ventilador tem, quando toda a potência elétrica do ventilador é convertida em taxa de energia cinética do ar. Ou seja, essa potência elétrica é toda usada para fazer de ar saírem, a cada segundo, do repouso (ar com velocidade zero) para uma velocidade . A figura abaixo mostra o caso.
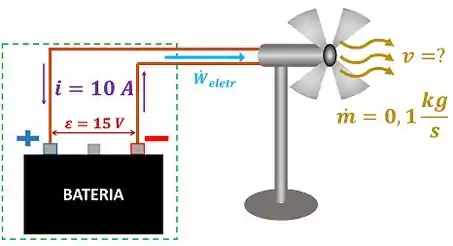
é a diferença de potencial elétrico da bateria, é a corrente elétrica que passa pelo circuito e é a massa de ar que passa pelo ventilador a cada segundo.
Achamos o valor da velocidade , igualando a potência elétrica com a taxa de energia cinética que o ar ganha através do ventilador.
Essa fórmula mostra que para achar , temos que achar primeiro. Por isso, calcularemos esse valor no próximo passo.
Passo 2
Então, querid@s, o valor da potência elétrica é obtido pela equação abaixo.
Substituindo esse valor na fórmula de , achamos:
Uhuuuuul! Achamos o valor da velocidade do ar que o ventilador movimenta!
Resposta
Exercício Resolvido #7
Elaboração própria
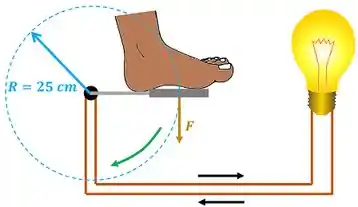
Em uma feira de ciências, é apresentada uma bicicleta que consegue acender uma lâmpada de , caso alguém use uma força para pedalar e gire o pedal com uma velocidade angular de . Considerando que a resistência da lâmpada vale , calcule a força necessária para acender a lâmpada.
Passo 1
Oi, gente! Como estão os estudos? Bora aproveitar essa animação pra fazer um exercício de potência elétrica?

A questão quer que a gente calcule a força que temos que fazer para acender a lâmpada, supondo que toda a potência de giro da roda da bicicleta é convertida potência elétrica da lâmpada. Ou seja, essa potência de giro da roda é toda usada para fazer a lâmpada acender através da dissipação de potência elétrica , como mostra a figura.
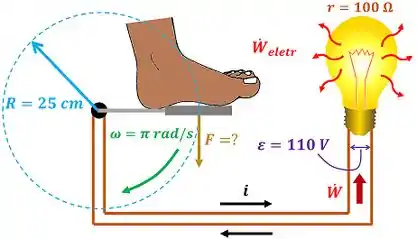
é a diferença de potencial elétrico da bateria, é a corrente elétrica que passa pelo circuito, é a resistência da lâmpada, é a velocidade angular da roda e é o raio do pedal.
Achamos o valor da força , igualando a potência de giro à potência elétrica . Lembre-se: a potência de giro é igual ao torque (força vezes raio ) vezes a velocidade .
Essa fórmula mostra que para achar , temos que achar primeiro. Por isso, calcularemos esse valor no próximo passo.
Passo 2
Então, querid@s, o valor da potência elétrica é obtido pela equação abaixo.
No entanto, não sabemos quanto vale o valor da corrente . Para calcular , precisamos usar a lei de Ohm abaixo.
Substituindo esse na equação de :
Antes de substituir , e na fórmula de , precisamos lembrar de converter de pra , dividindo ele por .
Shooooow! Encontramos o valor da força que faz a lâmpada acender!
Resposta
Exercício Resolvido #8
Elaboração própria
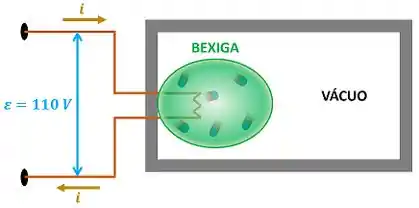
Uma câmara de possui uma bexiga cheia de gás perfeito a e . Essa bexiga possui uma resistência elétrica de em seu interior. Ao ligar essa resistência a uma fonte com de tensão por , o gás no interior da bexiga é aquecido até uma temperatura de . Por causa desse aquecimento, o gás se expande isobaricamente até estourar a bexiga e ocupar toda a câmara. Determine:
- a diferença entre o volume da câmara e o volume que a bexiga tinha logo antes de estourar;
- o trabalho total realizado pelo gás ao expandir dentro da bexiga e ao expandir por toda a câmara.
Passo 1
Como estão, chuchus?! Essa é uma questão que mistura dois temas: expansão não resistida e potência elétrica. Vamos resolver e ficar fera nesses assuntos?

Vamos sim, larga essa preguiça!
Primeiro, a questão quer saber quanto vale a diferença entre o volume da câmara e o volume que a bexiga tinha logo antes de estourar.
já foi informado pelo enunciado e vale . Logo, só resta encontrar pra calcular a resposta da letra (a) da questão. é encontrado, se a gente supor que toda a energia dissipada pela resistência elétrica é usada pelo gás para realizar o trabalho a pressão constante sobre a bexiga, fazendo ela crescer até estourar. A figura abaixo mostra isso.
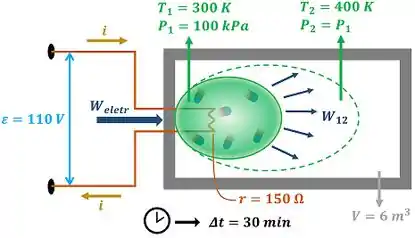
é a diferença de potencial elétrico da bateria, é a corrente elétrica que passa pelo circuito e é a resistência da lâmpada. e são a pressão e a temperatura do gás antes de expandir. e são a pressão e a temperatura do gás depois de expandir na bexiga.
Depois de tanta informação, vamos partir pra prática e resolver a letra (a)!
Passo 2
Como dito no passo 1, pra achar e calcular , temos que supor que a energia dissipada pela resistência é toda usada pra realizar um trabalho de movimento de fronteira sobre a bexiga. Logo, deve ser igual a .
Como é trabalho de movimento de fronteira a pressão constante, podemos calcular multiplicando a pressão pela variação de volume da bexiga . Além disso, o trabalho elétrico pode ser calculado multiplicando a potência elétrica pelo intervalo de tempo em que ela foi usada.
Para calcular , precisamos achar através da fórmula Pevetê Povotó de gases perfeitos.
Como , cortamos essas pressões e reorganizamos a equação pra achar .
Além disso, é igual a vezes . é encontrado através da lei de Ohm abaixo.
Vamos substituir todos esses dados na próxima etapa para achar e .
Passo 3
Substituindo as informações na segunda equação do passo 2:
Colocando em evidência:
Antes de substituir os valores, temos que converter a pressão de pra , multiplicando ela por e temos que converter de pra , multiplicando ele por
Substiuindo esse valor na equação de :
Essa é a resposta da letra (a). Então bora partir pra letra (b) e encerrar a questão!
Passo 4
O trabalho total é a soma do trabalho de expansão da bexiga e o trabalho de expansão do gás ao ocupar toda a câmara!
já pode ser encontrado pela fórmula abaixo.
Como o gás aumenta de volume e sua fronteira se expande, quando ele se difunde pela câmara, tendemos a achar que podemos calular o trabalho pela fórmula que calcula o trabalho de fronteira abaixo.
No entanto, usar essa fórmula é um erro, porque essa expansão devida ao rompimento da bexiga é uma expansão não resistida. Nesse caso, o gás não precisa vencer uma resistência para se expandir e ocupar o volume que estava em vácuo! Logo, o gás não precisa gastar energia e realizar trabalho para se mover. Ou seja, o trabalho que ele realiza vale !
Por isso, vale:
Ebaaaaaaa! Terminamos a questão! Encontramos a resposta da letra (b)!