Trabalho de Escoamento e Entalpia
Produzido por Philip Canabarro BlockerTeoria
Existem equações para calcular e ?
Vimos na teoria passada que a primeira lei da termodinâmica para volumes de controle pode ser escrita como:
Nós já sabemos que a taxa de trabalho pode ser calculada através de algumas equações específicas para cada tipo de trabalho. A taxa de calor também possui uma fórmula para cada tipo de transferência de calor. Existe alguma equação para calcular e ?
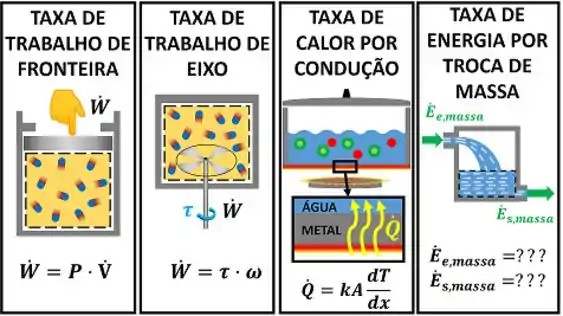
Sim! Existe uma equação para calcular e outra para calcular . Cada uma delas será explicada em detalhes a partir de agora! No entanto, para a explicação ficar mais fácil, usaremos um exemplo.
A fórmula para calcular pode ser dividida em duas partes
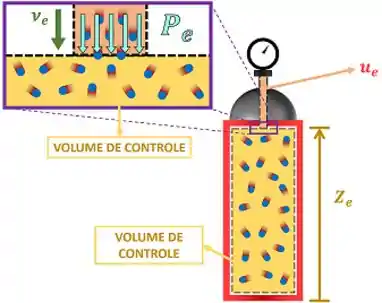
Imagine que estamos tentando encher um tanque rígido com gás. Considere que o nosso volume de controle seja sempre o gás que já está contido no tanque. No momento em que abrimos a válvula, uma vazão mássica começa a entrar no volume. Qual a taxa de energia que o volume de controle ganha com essa entrada de massa?
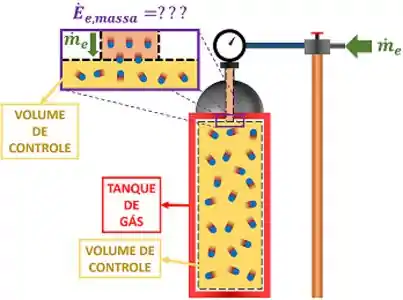
Podemos refazer essa pergunta para conseguir aplicar a primeira lei nesse exemplo. Qual é a taxa de variação da energia dentro do volume de controle , quando ele recebe uma vazão mássica ? Você pode notar que esse volume de controle não troca energia com a vizinhança por calor ou trabalho. Só por entrada massa. Logo, para esse volume de controle:
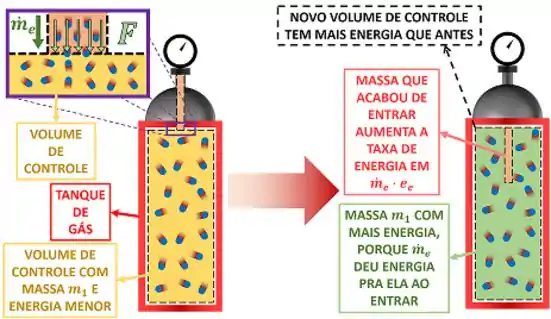
onde é a energia total contida dentro da vazão .
Vemos através da figura acima que o ganho de energia pode ser dividido em dois: uma parte é a energia contida na massa que está entrando . A outra parte é a energia que essa vazão dá pra massa que já está dentro , quando empurra ela para conseguir entrar. Quanto vale a taxa de energia que entra no volume através dessa segunda parte?
A segunda parte da fórmula de é a taxa de trabalho de escoamento
Vemos através da imagem anterior que a vazão tem que empurrar a massa que já está no volume de controle com uma força para conseguir entrar. Isso significa que a vazão está realizando trabalho na massa . Chamamos esse trabalho de trabalho de escoamento . Mas como podemos fazer o cálculo desse novo tipo de trabalho?
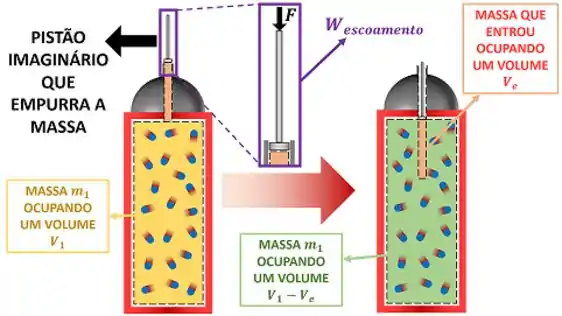
Como está mostrado na figura de cima, esse trabalho é igualzinho ao trabalho que o pistão realiza sobre um gás, quando empurra ele. Por isso, podemos usar a mesma fórmula que utilizamos para o trabalho de um pistão.
onde:
- é a pressão do gás que está entrando;
- é a variação do volume da massa , quando o gás entra.
A massa que já estava no volume de controle é comprimida, porque um volume de gás acabou de entrar e dividir espaço com a massa que estava sozinha antes. Portanto, o volume de perdeu um espaço igual a . Logo:
Podemos calcular o volume através do volume específico da massa que está entrando.
Por causa disso, o trabalho de escoamento passa a ter uma nova fórmula:
Esse é o trabalho total realizado sobre o volume de controle, quando a massa entra nele. Como podemos calcular o trabalho realizado sobre o volume de controle por segundo, quando a vazão entra no seu espaço?

Se o trabalho de escoamento é calculado multiplicando pela quantidade de massa que entra , então o trabalho de escoamento por segundo é calculado multiplicando pela quantidade de massa que entra por segundo .
onde é a taxa de trabalho de escoamento sobre o volume de controle. Sua unidade no Sistema Internacional (S.I.) é o joule por segundo ou o watt .
Ou seja, ela é calculada substituindo a massa pela vazão .
A soma das duas partes de é a entalpia específica da vazão de entrada
Agora que temos uma fórmula para cada parte de queremos saber qual é a fórmula de total. Essa taxa de energia que entra no volume de controle é igual à taxa de trabalho de escoamento mais a energia da vazão que entra no volume de controle .
onde:
- é a energia interna específica da massa que está entrando no volume de controle. Sua unidade no Sistema Internacional de Unidades é o joule por quilograma ;
- é a velocidade da massa que está entrando no volume de controle. Sua unidade no Sistema Internacional de Unidades é o metro por segundo ;
- é a altura da massa que está entrando no volume de controle. Sua unidade no Sistema Internacional de Unidades é o metro .
Deixando a vazão de entrada em evidência e juntando as duas partes, a equação vira:
Vemos na fórmula que a soma dos dois pedaços fez a entalpia específica da massa que está entrando no volume de controle aparecer! Ou seja, a entalpia ganha um novo significado! Ela é a soma da energia interna específica da substância mais o seu trabalho de escoamento ! Com isso:
Pronto, achamos a fórmula da taxa de energia que entra no volume de controle por conta da entrada de massa . Agora só precisamos encontrar para conhecer a primeira lei de volume de controle completa. Então vamos fazer isso agora!
A fórmula para calcular
Para encontrar uma equação para a taxa de energia que sai do volume de controle junto com a vazão de saída , nós temos que cumprir as mesmas etapas! Só o exemplo inicial que vai mudar. Agora, vamos imaginar um tanque rígido sendo esvaziado. Qual é a taxa de energia que o volume de controle perde com essa saída de massa a uma vazão ?
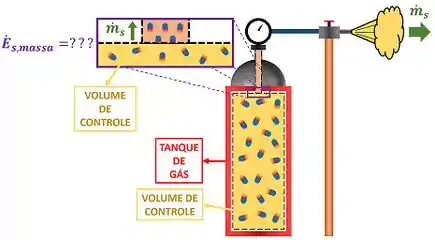
Assim como , também pode ser dividido em duas partes. Além disso, a segunda parte também é a taxa de trabalho de escoamento . Então espera aí! Se esses dois termos tem tantas características em comum, será que têm equações iguaizinhas? Saber disso facilitaria muito, porque evitaria todo aquele passo a passo para achar uma só equação!

Esse chute foi certeiro! Esses dois termos são bem parecidos! A única adaptação que precisamos fazer é mudar o índice “” da equação de , que indica a massa que entra, pelo índice “s” que indica a massa que sai!
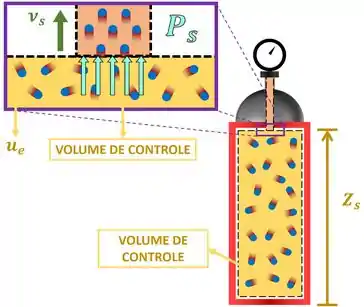
A fórmula final da primeira lei para volumes de controle
Substituindo as fórmulas de e na equação de conservação de energia para o volume de controle, chegamos na fórmula completa da primeira lei para volume de controle.
Calma, eu sei que essa equação é enorme! No entanto, na maioria das vezes, a gente vai usar uma forma menor dessa equação. Geralmente, a diferença de altura da massa que entra e da massa que sai são desprezíveis. A diferença de velocidade entre essas duas massas também é desprezada em vários casos. Por causa disso, a fórmula pode ser reduzida para:
A segunda parte da fórmula de E ˙ e , m a s s a é a taxa de trabalho de escoamento W ˙ e s c o a m e n t o
A soma das duas partes de E ˙ e , m a s s a é a entalpia específica da vazão de entrada h e
A fórmula para calcular E ˙ s , m a s s a
A fórmula final da primeira lei para volumes de controle
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
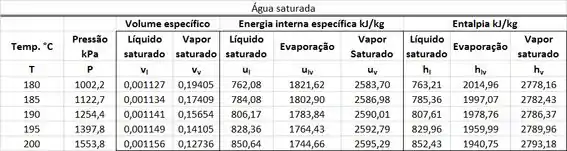
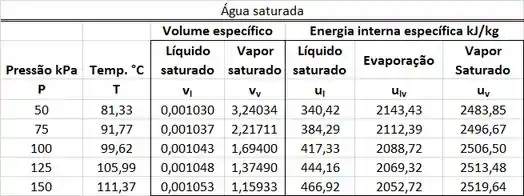
Um tanque rígido contendo vapor d’água vaza de vapor d’água saturado a . Calcule a taxa de energia que o tanque rígido perde devido à saída desse vapor. Use a tabela abaixo. Considere a energia cinética e a energia potencial do vapor saturado desprezíveis.
Passo 1
O enunciado pede que a gente calcule o valor da taxa de energia que o tanque rígido perde devido à saída desse vapor. A figura abaixo mostra todos os dados que temos para calcular o valor de .
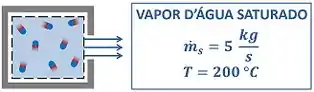
é a temperatura do vapor saturado d’água e é a vazão mássica do vapor saindo do tanque.
No próximo passo, veremos qual fórmula é usada para calcular .
Passo 2
A taxa de energia que o tanque rígido perde devido à saída desse vapor é calculada pela fórmula abaixo. A energia cinética e a energia potencial do vapor não estão presentes nessa fórmula, porque o enunciado informou que seus valores são tão pequenos que podemos desprezá-los.
onde é a entalpia específica do vapor saturado saindo no tanque rígido.
O valor de está presente na tabela de saturação. está na mesma linha que a temperatura de e na mesma coluna que a entalpia específica do vapor saturado .

Agora que sabemos como encontrar o valor de todos os termos, vamos começar a fazer contas!
Passo 3
O valor de é obtido abaixo!
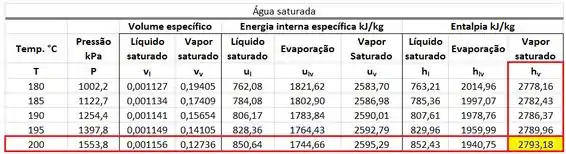
Usando esses valores na fórmula de , encontramos:
Resposta
Exercício Resolvido #2
Elaboração própria
Um tanque rígido contendo vapor d’água recebe de vapor d’água saturado a . Calcule a taxa de trabalho de escoamento do vapor d’água saturado que entra no tanque. Use a tabela abaixo.
Passo 1
O enunciado pede que a gente calcule o valor da taxa de trabalho de escoamento do vapor d’água saturado. Esse vapor saturado realiza trabalho empurrando o vapor presente no tanque. Ele faz isso para abrir espaço no tanque e entrar no volume de controle. A figura abaixo mostra todos os dados que temos para calcular esse valor.
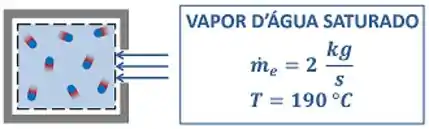
é a temperatura do vapor saturado d’água e é a vazão mássica do vapor entrando no tanque.
No próximo passo, veremos qual fórmula é usada para calcular a taxa de trabalho de escoamento.
Passo 2
A taxa de trabalho de escoamento é calculada pela fórmula abaixo.
onde é a pressão do vapor saturado e é o volume específico do vapor saturado.
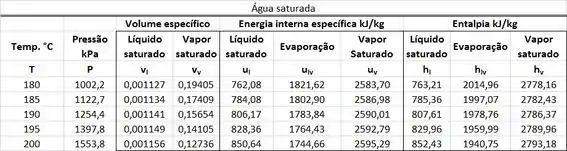
Os valores de e estão presentes na tabela de saturação. está na mesma linha que a temperatura de e na mesma coluna que o volume específico . está na mesma linha que a temperatura de e na mesma coluna que a pressão .

Agora que sabemos como encontrar o valor de todos os termos, vamos começar a fazer contas!
Passo 3
Os valores de e são obtidos abaixo!
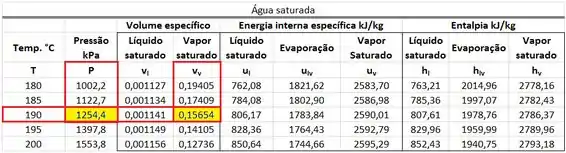
Usando esses valores na fórmula de trabalho de escoamento, encontramos:
Resposta
Exercício Resolvido #3
Elaboração própria
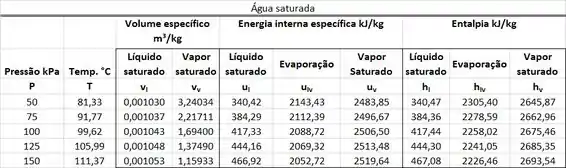
Água líquida saturada a entra em um tanque rígido com uma velocidade de através de uma tubulação com de diâmetro. A água é aquecida dentro do tanque e sai dele como vapor saturado a com uma velocidade de por um tubo com de diâmetro. Considerando a energia potencial da água desprezível, calcule a taxa de variação da energia do tanque rígido devido à entrada e à saída de água.
Passo 1
O enunciado pede que a gente calcule o valor da taxa de variação da energia do tanque rígido devido à entrada e à saída de água . Perceba que o tanque também recebe energia por calor, porque é aquecido. No entanto, o enunciado só quer saber da parcela de energia que o tanque troca através da entrada e da saída de água. A figura abaixo mostra todos os dados que temos para calcular esse valor.
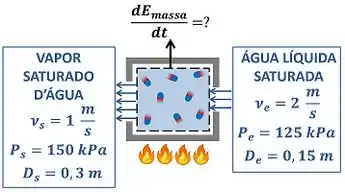
é a velocidade da água líquida saturada entrando no tanque rígido por um tubo de diâmetro igual a . é a pressão da água entrado no tanque rígido. é a velocidade do vapor saturado d’água saindo do tanque rígido por um tubo de diâmetro igual a . é a pressão desse vapor.
No próximo passo, veremos qual fórmula é usada para calcular .
Passo 2
A fórmula da taxa de variação da energia do tanque devido à entrada e saída de massa se encontra abaixo.
onde é a taxa de energia que entra no tanque por causa de entrada de água e é a taxa de energia que sai no tanque por causa de saída de água.
As fórmulas de e encontram-se abaixo. A energia potencial da água não está presente nessas fórmulas, porque o enunciado falou que ela é desprezível.
é a vazão mássica e é a entalpia específica da água líquida que entra no tanque. é a vazão mássica, é o volume específico e é a entalpia específica do vapor d’água que sai do tanque.
No próximo passo vamos aprender como encontrar os valores de alguns termos das fórmulas!
Passo 3
e são calculadas por fórmulas muito parecidas! Os dois são igual à massa específica da água multiplicada pela velocidade da água multiplicada pela área de passagem da água . Esse área pode ser calculada através do diâmetro do tubo pelo qual a água passa.
Além disso, as massas específicas são o inverso dos volumes específicos.
é o volume específico da água líquida que entra no tanque e é o volume específico do vapor d’água que sai do tanque.
Agora que conhecemos essas fórmulas, temos que aprender a encontrar os valores de , , e .
Passo 4
Os valores de , , e estão presentes na tabela de saturação. está na mesma linha que a pressão de e na mesma coluna que o volume específico . está na mesma linha que a pressão de e na mesma coluna que o volume específico . está na mesma linha que a pressão de e na mesma coluna que a entalpia específica . está na mesma linha que a pressão de e na mesma coluna que a entalpia específica .

Agora que aprendemos tudo isso, podemos começar a fazer as contas!
Passo 5
A primeira parte dos cálculos é de encontrar , , e na tabela de saturação. e são obtidos abaixo.
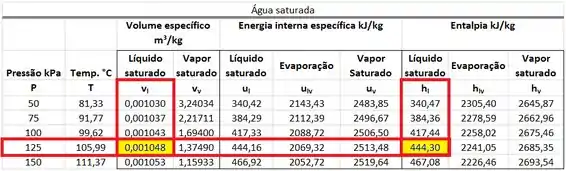
e são obtidos abaixo.
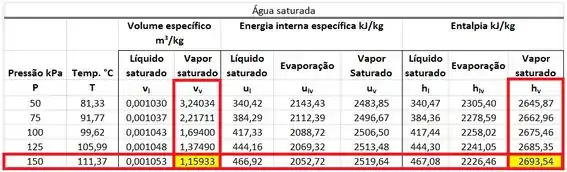
No próximo passo, vamos calcular as vazões e a taxa de variação de energia do tanque .
Passo 6
Começamos os cálculos das vazões pelo cálculo das massas específicas.
Com esses valores, podemos achas as vazões mássicas.
Agora podemos encontrar e .
Cuidado! Para a parcela de energia cinética ficar na unidade certa na fómula de e , precisamos dividir a parcela por mil!
Por fim, vale:
Resposta
Exercício Resolvido #4
Elaboração própria
Água líquida saturada a entra em um tanque rígido com uma velocidade de através de uma tubulação com de diâmetro. A água é aquecida dentro do tanque e sai dele como vapor saturado a com uma velocidade de por um tubo com de diâmetro. Considerando a energia potencial da água desprezível, calcule a taxa de variação da energia do tanque rígido devido à entrada e à saída de água.
Passo 1
O enunciado pede que a gente calcule o valor da taxa de variação da energia do tanque rígido devido à entrada e à saída de água . Perceba que o tanque também recebe energia por calor, porque é aquecido. No entanto, o enunciado só quer saber da parcela de energia que o tanque troca através da entrada e da saída de água. A figura abaixo mostra todos os dados que temos para calcular esse valor.
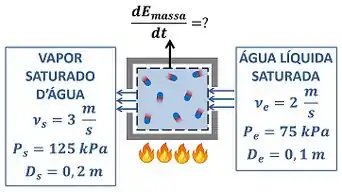
é a velocidade da água líquida saturada entrando no tanque rígido por um tubo de diâmetro igual a . é a pressão da água entrado no tanque rígido. é a velocidade do vapor saturado d’água saindo do tanque rígido por um tubo de diâmetro igual a . é a pressão desse vapor.
No próximo passo, veremos qual fórmula é usada para calcular .
Passo 2
A fórmula da taxa de variação da energia do tanque devido à entrada e saída de massa se encontra abaixo.
onde é a taxa de energia que entra no tanque por causa de entrada de água e é a taxa de energia que sai no tanque por causa de saída de água.
As fórmulas de e encontram-se abaixo. A energia potencial da água não está presente nessas fórmulas, porque o enunciado falou que ela é desprezível.
é a vazão mássica, é o volume específico e é a energia interna específica da água líquida que entra no tanque. é a vazão mássica, é o volume específico e é a energia interna específica do vapor d’água que sai do tanque.
No próximo passo vamos aprender como encontrar os valores de alguns termos das fórmulas!
Passo 3
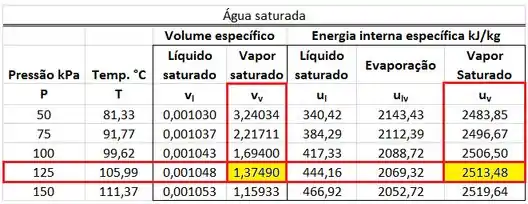
Os valores de , , e estão presentes na tabela de saturação. está na mesma linha que a pressão de e na mesma coluna que o volume específico . está na mesma linha que a pressão de e na mesma coluna que o volume específico . está na mesma linha que a pressão de e na mesma coluna que a energia interna específica . está na mesma linha que a pressão de e na mesma coluna que a energia interna específica .

Vamos aprender a calcular e no passo seguinte!
Passo 4
e são calculadas por fórmulas muito parecidas! Os dois são igual à massa específica da água multiplicada pela velocidade da água multiplicada pela área de passagem da água . Esse área pode ser calculada através do diâmetro do tubo pelo qual a água passa.
Além disso, as massas específicas são o inverso dos volumes específicos.
Agora que aprendemos tudo isso, podemos começar a fazer as contas!
Passo 5
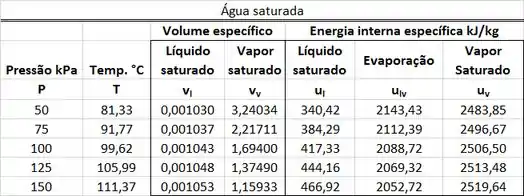
A primeira parte dos cálculos é de encontrar , , e na tabela de saturação. e são obtidos abaixo.
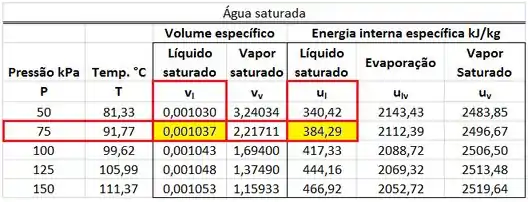
e são obtidos abaixo.
No próximo passo, vamos calcular as vazões e a taxa de variação de energia do tanque .
Passo 6
Começamos os cálculos das vazões pelo cálculo das massas específicas.
Com esses valores, podemos achas as vazões mássicas.
Agora podemos encontrar e .
Cuidado! Para a parcela de energia cinética ficar na unidade certa na fómula de e , precisamos dividir a parcela por mil!
Por fim, vale:
Resposta
Exercício Resolvido #5
Elaboração própria
Água líquida saturada a entra em um tanque rígido com uma velocidade de através de uma tubulação com e a uma altura de em relação ao solo. A água sai do tanque como líquido saturado a com uma velocidade de por um tubo com de diâmetro e a uma altura de em relação ao solo. Determine a taxa de variação da energia do tanque rígido devido à entrada e à saída de água.
Passo 1
O enunciado pede que a gente calcule o valor da taxa de variação da energia do tanque rígido devido à entrada e à saída de água . Ou seja, o enunciado só quer saber da parcela de energia que o tanque troca através da entrada e da saída de água. Ele não está interessado na troca de energia por calor ou trabalho com o ambiente. A figura abaixo mostra todos os dados que temos para calcular esse valor.
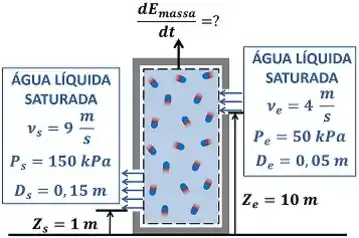
é a velocidade da água entrando no tanque rígido por um tubo de diâmetro igual a a uma altura do chão. é a pressão da água entrado no tanque rígido. é a velocidade da água saindo do tanque rígido por um tubo de diâmetro igual a a uma altura do chão. é a pressão dessa água. No próximo passo, veremos qual fórmula é usada para calcular .
Passo 2
A fórmula da taxa de variação da energia do tanque devido à entrada e saída de massa se encontra abaixo.
onde é a taxa de energia que entra no tanque por causa de entrada de água e é a taxa de energia que sai no tanque por causa de saída de água.
As fórmulas de e encontram-se abaixo.
é a vazão mássica, é o volume específico e é a energia interna específica da água que entra no tanque. é a vazão mássica, é o volume específico e é a energia interna específica da água que sai do tanque. é a aceleração da gravidade da Terra.
No próximo passo vamos aprender como encontrar os valores de alguns termos das fórmulas!
Passo 3
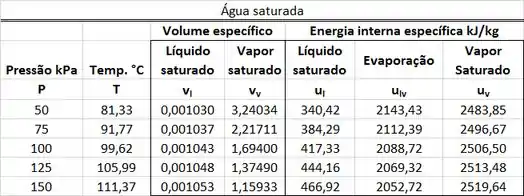
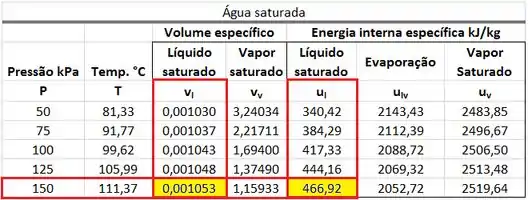
Os valores de , , e estão presentes na tabela de saturação. está na mesma linha que a pressão de e na mesma coluna que o volume específico . está na mesma linha que a pressão de e na mesma coluna que o volume específico .

está na mesma linha que a pressão de e na mesma coluna que a energia interna específica . está na mesma linha que a pressão de e na mesma coluna que a energia interna específica .
Vamos aprender a calcular e no passo seguinte!
Passo 4
e são calculadas por fórmulas muito parecidas! Os dois são igual à massa específica da água multiplicada pela velocidade da água multiplicada pela área de passagem da água . Esse área pode ser calculada através do diâmetro do tubo pelo qual a água passa.
Além disso, as massas específicas são o inverso dos volumes específicos.
Agora que aprendemos tudo isso, podemos começar a fazer as contas!
Passo 5
A primeira parte dos cálculos é de encontrar , , e na tabela de saturação. e são obtidos abaixo.
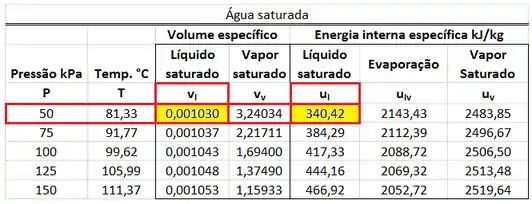
e são obtidos abaixo.
No próximo passo, vamos calcular as vazões, e .
Passo 6
Começamos os cálculos das vazões pelo cálculo das massas específicas.
Com esses valores, podemos achas as vazões mássicas.
Agora podemos encontrar e .
Cuidado! Para as parcelas de energia potencial e energia cinética ficarem na unidade certa na fómula de , precisamos dividir cada uma dessas parcelas por mil!
Vamos partir para o cálculo de e da taxa de variação de energia do tanque !
Passo 7
Cuidado! Para as parcelas de energia potencial e energia cinética ficarem na unidade certa na fómula de , precisamos dividir cada uma dessas parcelas por mil!
Por fim, vale:
Resposta
Exercício Resolvido #6
Elaboração própria
Água líquida saturada a entra em um tanque rígido com uma velocidade de através de uma tubulação com e a uma altura de em relação ao solo. A água recebe calor dentro do tanque a uma taxa de . Ela sai do tanque como vapor saturado a mesma pressão da sua entrada, com uma velocidade de por um tubo com de diâmetro e a uma altura de em relação ao solo. Determine a taxa de variação da energia do tanque rígido.
Passo 1
O enunciado pede que a gente calcule o valor da taxa de variação da energia do tanque rígido . A figura abaixo mostra todos os dados que temos para calcular esse valor.
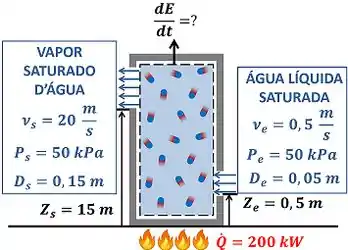
é a velocidade da água entrando no tanque rígido por um tubo de diâmetro igual a a uma altura do chão. é a pressão da água entrado no tanque rígido. é a velocidade do vapor d’água saindo do tanque rígido por um tubo de diâmetro igual a a uma altura do chão. é a pressão dessa água. é a taxa de calor que a água recebe.
No próximo passo, veremos qual fórmula é usada para calcular .
Passo 2
A fórmula da taxa de variação da energia do tanque se encontra abaixo. Ela é a primeira lei da termodinâmica aplicada ao volume de controle.
onde é a taxa de energia que entra no tanque por causa de entrada de água, é a taxa de energia que sai no tanque por causa de saída de água e é a taxa de trabalho que a água do tanque realiza.
As fórmulas de e encontram-se abaixo.
é a vazão mássica, é o volume específico e é a energia interna específica da água que entra no tanque. é a vazão mássica, é o volume específico e é a energia interna específica do vapor d’água que sai do tanque. é a aceleração da gravidade da Terra.
No próximo passo vamos aprender como encontrar os valores de alguns termos das fórmulas!
Passo 3
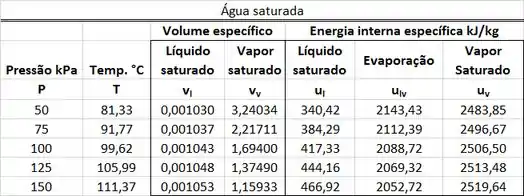
Os valores de , , e estão presentes na tabela de saturação. está na mesma linha que a pressão de e na mesma coluna que o volume específico . está na mesma linha que a pressão de e na mesma coluna que o volume específico .

está na mesma linha que a pressão de e na mesma coluna que a energia interna específica . está na mesma linha que a pressão de e na mesma coluna que a energia interna específica .
Vamos aprender a calcular e no passo seguinte!
Passo 4
e são calculadas por fórmulas muito parecidas! Os dois são igual à massa específica da água multiplicada pela velocidade da água multiplicada pela área de passagem da água . Esse área pode ser calculada através do diâmetro do tubo pelo qual a água passa.
Além disso, as massas específicas são o inverso dos volumes específicos.
Agora só falta aprender a calcular para poder iniciar as contas.
Passo 5
Na verdade, não vai precisar ser calculado!

Como a água está dentro de um tanque rígido e ela está mudando de fase, ela sempre ocupa o mesmo volume. Isso quer dizer que a fronteira da água do tanque não se movimenta. Ou seja, não existe trabalho por movimento de fronteira nesse problema! Por conta disso:
Agora que aprendemos tudo isso, podemos começar a fazer as contas!
Passo 6
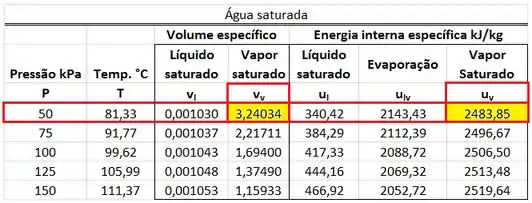
A primeira parte dos cálculos é de encontrar , , e na tabela de saturação. e são obtidos abaixo.
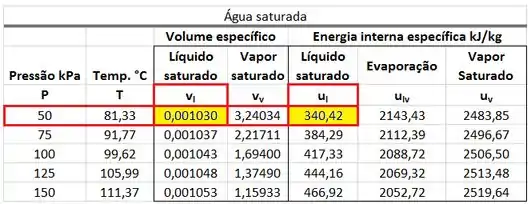
e são obtidos abaixo.
No próximo passo, vamos calcular as vazões e .
Passo 7
Começamos os cálculos das vazões pelo cálculo das massas específicas.
Com esses valores, podemos achas as vazões mássicas.
Agora podemos encontrar e .
Cuidado! Para as parcelas de energia potencial e energia cinética ficarem na unidade certa na fómula de , precisamos dividir cada uma dessas parcelas por mil!
Vamos partir para o cálculo de e da taxa de variação de energia do tanque !
Passo 8
Cuidado! Para as parcelas de energia potencial e energia cinética ficarem na unidade certa na fómula de , precisamos dividir cada uma dessas parcelas por mil!
Por fim, vale:
Resposta
Exercício Resolvido #7
Elaboração própria
Água líquida saturada a entra em um tanque rígido com uma velocidade de através de uma tubulação com e a uma altura de em relação ao solo. A água sai do tanque como líquido saturado a mesma pressão da sua entrada, com uma velocidade de por um tubo com de diâmetro e a uma altura de em relação ao solo. Determine a taxa de variação da energia do tanque rígido, considerando que a água do interior do tanque também permanece saturada a a todo momento e que todo o processo é adiabático.
Passo 1
O enunciado pede que a gente calcule o valor da taxa de variação da energia do tanque rígido . A figura abaixo mostra todos os dados que temos para calcular esse valor.
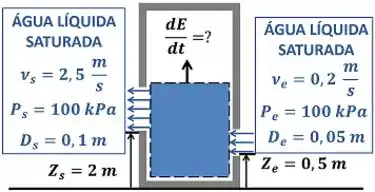
é a velocidade da água entrando no tanque rígido por um tubo de diâmetro igual a a uma altura do chão. é a pressão da água entrado no tanque rígido. é a velocidade da água saindo do tanque rígido por um tubo de diâmetro igual a a uma altura do chão. é a pressão dessa água.
No próximo passo, veremos qual fórmula é usada para calcular .
Passo 2
A fórmula da taxa de variação da energia do tanque se encontra abaixo. Ela é a primeira lei da termodinâmica aplicada ao volume de controle.
onde é a taxa de energia que entra no tanque por causa de entrada de água, é a taxa de energia que sai no tanque por causa de saída de água e é a taxa de trabalho que a água do tanque realiza.
As fórmulas de e encontram-se abaixo.
é a vazão mássica, é o volume específico e é a energia interna específica da água que entra no tanque. é a vazão mássica, é o volume específico e é a energia interna específica da água que sai do tanque. é a aceleração da gravidade da Terra.
No próximo passo vamos aprender como encontrar os valores de alguns termos das fórmulas!
Passo 3
Os valores de , , e estão presentes na tabela de saturação. está na mesma linha que a pressão de e na mesma coluna que o volume específico . é igual a , porque a água que entra e a água que sai estão no mesmo estado!

e estão na mesma linha que a pressão de e na mesma coluna que a energia interna específica .
Vamos aprender a calcular , e no passo seguinte!
Passo 4
Na verdade, não precisa ser calculado! Como o enunciado diz que o processo de troca de massa com o ambiente é adiabático, vale zero.
e são calculadas por fórmulas muito parecidas! Os dois são igual à massa específica da água multiplicada pela velocidade da água multiplicada pela área de passagem da água . Esse área pode ser calculada através do diâmetro do tubo pelo qual a água passa.
Além disso, as massas específicas são o inverso dos volumes específicos.
Passo 5
Como o tanque recebe e rejeita quantidades diferentes de água líquida, o volume de água do tanque varia a uma taxa igual a . Isso significa que a fronteira da água do tanque se mexe e a água realiza trabalho por movimento de fronteira a uma taxa igual a .

Como o enunciado diz que a água permanece sempre a mesma pressão de , esse trabalho é isobárico. Logo, a quantidade de energia por trabalho que o vapor recebe , quando a fronteira se movimenta pode ser calculado pela seguinte fórmula.
é a variação de volume da água do tanque. No entanto, nós não sabemos quando vale nem . Então como fazemos para transformar essa fórmula em uma equação que tenha o dado informado pelo enunciado () e a taxa de trabalho precisamos achar ?

O primeiro passo para transformar a fórmula antiga é dividir todos os termos dessa equação pelo intervalo de tempo de duração processo .
O passo final é fazer o intervalo de tempo ficar cada vez menor. No limite, quando tende a zero, essas divisões viram derivadas! Ou seja, elas viram as taxas de variação em relação ao tempo!
será calculada no próximo passo.
Passo 6
pode ser calculada através da equação de conservação de massa para volumes de controle.
No entanto, a massa específica da água do tanque é constante e vale a mesma coisa que a massa específica , porque as duas águas estão saturadas a . Por isso:
Substituindo essa equação na fórmula de , encontramos uma nova fórmula para .
Agora que aprendemos tudo isso, podemos começar a fazer as contas!
Passo 7
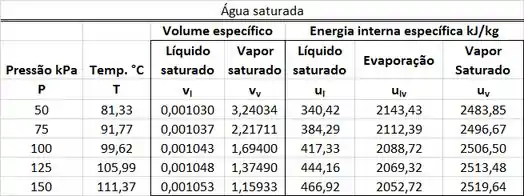
A primeira parte dos cálculos é de encontrar , , e na tabela de saturação.
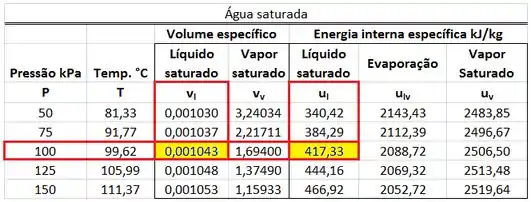
No próximo passo, vamos calcular as vazões e .
Passo 8
Começamos os cálculos das vazões pelo cálculo das massas específicas.
Com esses valores, podemos achas as vazões mássicas.
Agora podemos encontrar e .
Cuidado! Para as parcelas de energia potencial e energia cinética ficarem na unidade certa na fómula de , precisamos dividir cada uma dessas parcelas por mil!
Vamos partir para o cálculo de , de e da taxa de variação de energia do tanque !
Passo 9
Cuidado! Para as parcelas de energia potencial e energia cinética ficarem na unidade certa na fómula de , precisamos dividir cada uma dessas parcelas por mil!
pode ser achado a partir da fórmula que criamos.
Por fim, vale:
Resposta
Exercício Resolvido #8
Elaboração própria
Água líquida saturada a entra em um tanque rígido com uma velocidade de através de uma tubulação com e a uma altura de em relação ao solo. A água sai do tanque como líquido saturado a mesma pressão da sua entrada por um tubo com de diâmetro e a uma altura de em relação ao solo. A área da seção transversal do tanque rígido vale . O nível da água do tanque desce a uma velocidade de . Determine a taxa de variação da energia da água do tanque rígido, considerando que a água do interior do tanque também permanece saturada a a todo momento e que todo o processo é adiabático.
Passo 1
O enunciado pede que a gente calcule o valor da taxa de variação da energia da água do tanque rígido . A figura abaixo mostra todos os dados que temos para calcular esse valor.
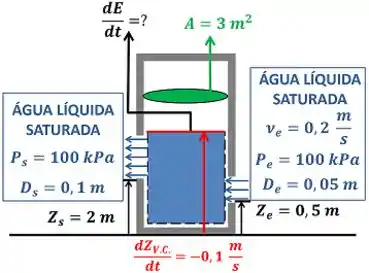
é a velocidade da água entrando no tanque rígido por um tubo de diâmetro igual a a uma altura do chão. é a pressão da água entrado no tanque rígido. A água sai do tanque rígido por um tubo de diâmetro igual a a uma altura do chão. é a pressão dessa água. é a área da seção transversal e é a velocidade com a qual o nível da água do tanque desce.
Ela é negativa, porque a altura desce. Logo, a altura varia negativamente.

Calcularemos através da primeira lei da termodinâmica aplicada ao volume de controle. No próximo passo, veremos essa equação.
Passo 2
A fórmula da taxa de variação da energia do tanque se encontra abaixo. Ela é a primeira lei da termodinâmica aplicada ao volume de controle.
onde é a taxa de energia que entra no tanque por causa de entrada de água, é a taxa de energia que sai no tanque por causa de saída de água e é a taxa de trabalho que a água do tanque realiza.
As fórmulas de e encontram-se abaixo.
é a vazão mássica, é o volume específico e é a energia interna específica da água que entra no tanque. é a vazão mássica, é o volume específico, é a energia interna específica e é a velocidade da água que sai do tanque. é a aceleração da gravidade da Terra.
No próximo passo vamos aprender como encontrar os valores de alguns termos das fórmulas!
Passo 3
Os valores de , , e estão presentes na tabela de saturação. está na mesma linha que a pressão de e na mesma coluna que o volume específico . é igual a , porque a água que entra e a água que sai estão no mesmo estado!

e estão na mesma linha que a pressão de e na mesma coluna que a energia interna específica .
Vamos aprender a calcular e no passo seguinte!
Passo 4
Na verdade, não precisa ser calculado! Como o enunciado diz que o processo de troca de massa com o ambiente é adiabático, vale zero.
é igual à massa específica da água multiplicada pela velocidade da água multiplicada pela área de passagem da água . Esse área pode ser calculada através do diâmetro do tubo pelo qual a água passa.
Além disso, as massas específicas são o inverso dos volumes específicos.
Passo 5
Como o tanque recebe e rejeita quantidades diferentes de água líquida, o volume de água do tanque varia a uma taxa igual a . Isso significa que a fronteira da água do tanque se mexe e a água realiza trabalho por movimento de fronteira a uma taxa igual a .

Como o enunciado diz que a água permanece sempre a mesma pressão de , esse trabalho é isobárico. Logo, a quantidade de energia por trabalho que o vapor recebe , quando a fronteira se movimenta pode ser calculado pela seguinte fórmula.
é a variação de volume da água do tanque. No entanto, nós não sabemos quando vale nem . Então como fazemos para transformar essa fórmula em uma equação que tenha o dado informado pelo enunciado () e a taxa de trabalho precisamos achar ?

O primeiro passo para transformar a fórmula antiga é dividir todos os termos dessa equação pelo intervalo de tempo de duração processo .
O passo final é fazer o intervalo de tempo ficar cada vez menor. No limite, quando tende a zero, essas divisões viram derivadas! Ou seja, elas viram as taxas de variação em relação ao tempo!
, e serão calculadas no próximo passo.
Passo 6
pode ser calculada através da equação de conservação de massa para volumes de controle.
No entanto, a massa específica da água do tanque é constante e vale a mesma coisa que a massa específica , porque as duas águas estão saturadas a . Por isso:
No entanto o volume é igual à área da seção transversal do tanque vezes a altura da água presente nele . Por causa disso, achamos uma fórmula para .
A vazão mássica da água que sai do tanque também pode ser calculada por uma fórmula muito parecida com a fórmula de . Com essa equação, conseguimos criar uma fórmula para .
Agora que aprendemos tudo isso, podemos começar a fazer as contas!
Passo 7
A primeira parte dos cálculos é de encontrar , , e na tabela de saturação.
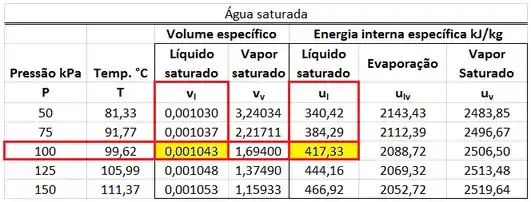
No próximo passo, vamos calcular as vazões.
Passo 8
Começamos os cálculos das vazões pelo cálculo das massas específicas.
Com esses valores, podemos achas as vazões mássicas.
Sabendo essa vazão, podemos calcular e .
Agora podemos encontrar e .
Passo 9
Cuidado! Para as parcelas de energia potencial e energia cinética ficarem na unidade certa na fómula de , precisamos dividir cada uma dessas parcelas por mil!
Cuidado! Para as parcelas de energia potencial e energia cinética ficarem na unidade certa na fómula de , precisamos dividir cada uma dessas parcelas por mil!
Vamos partir para o cálculo de e da taxa de variação de energia do tanque !
Passo 10
pode ser achado a partir da fórmula:
No entanto pode ser calculado pela fórmula:
Logo:
Substituindo os dados que conhecemos, encontramos:
Por fim, vale: