Processo em Regime Permanente
Produzido por Philip Canabarro BlockerTeoria
Fala aí! Neste textinho, vamos aprender sobre processos em regime permanente.
Se você tá estudando Mecânica dos Fluidos e caiu aqui de paraquedas, sinto em te informar que aqui estaremos mais focados na termodinâmica. Mas não se preocupa! Eu já tenho esse conteúdo explicadinho e separado aqui pra você, junto com alguns outros links de conceitos que são bem importantes você estar dominando antes de darmos sequência aqui.
E vai uma dica: muita coisa que veremos aqui também vale lá para a MecFlu (inclusive uma dica super importante que vou dar lá no final), então se eu fosse você, eu ficaria.
Se liga 👇😗
- O que é um escoamento em regime permanente?
- Conservação de massa.
- Conservação de energia e primeira lei da termodinâmica.
- As leis da termodinâmica: resumo e fórmulas.
O que é um processo em regime permanente?
O processo em regime permanente vai resolver uma dificuldade muito grande que encontramos quando vamos usar duas equações extremamente importantes da termodinâmica.
As equações que tô falando são essas aqui 👇
Equação da conservação de massa:
E da conservação de energia:
Essas fórmulas são muito úteis e usadas em quase todos os volumes de controle que estudamos. Mas acontece que, geralmente, não sabemos como a massa do volume de controle
E é aí que entra o processo em regime permanente! Esse tipo de processo garante que toda a massa e a energia que entra no sistema será igual à que sai. Quer dizer que essas derivadas valem zero!
Além disso, a diferença de altura
E:
Lembrando: só vamos fazer essas considerações se o enunciado nos disse que o processo está em regime permanente, beleza?
Mais simplificações em um processo de regime permanente
A mesma pergunta que fizemos para
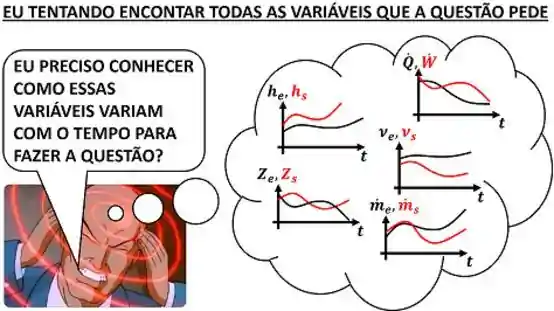
De forma alguma! Em um processo de regime permanente, nenhuma propriedade do volume de controle varia com o tempo. Além disso, as propriedades da massa que entra e da massa que sai também permanecem constantes durante o processo! E o mesmo vale para as vazões mássicas e as taxas de transferência de energia: elas também não variam com o tempo.
Sacou o quanto é legal sabermos da definição de um processo em regime permanente? Isso vai ajudar bastante nos nossos cálculos para os exercícios.
Por falar nisso, bora ver na prática como fica um exercício disso resolvido passo a passo.
A água fria entra no chuveiro com entalpia específica
Imagine um chuveiro com aquecimento elétrico. Considere que esse aquecimento ocorre em regime permanente.
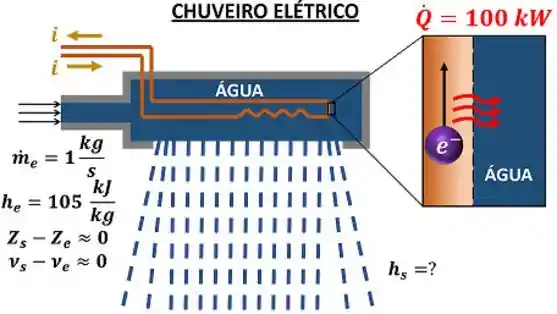
Beleza, se o exercício nos deu a vazão mássica de entrada, podemos começar os cálculos descobrindo a vazão mássica de saída.
Passo 1: Encontrar a vazão mássica de saída por meio da equação de conservação de massa.
Passo 2: Substituir os valores conhecidos na primeira lei da termodinâmica.
Na equação de conservação de energia, o termo
Passo 3: Interpretação do resultado.
Esse resultado mostra que a água que entrou no volume de controle aumentou sua entalpia, depois que recebeu calor da resistência elétrica. Como a entalpia é a energia interna mais o trabalho de escoamento, ela também é uma forma de energia!
Mas, pera aí, se a energia da água aumentou nesse processo, por que perdemos tempo falando que a energia total do volume de controle permanecia constante em um processo em regime permanente? Já vamos tirar essa dúvida a seguir!
As propriedades de cada ponto do volume de controle em regime permanente são constantes
Ao longo do seu caminho, a molécula de água vai recebendo calor da resistência quente e sua energia aumenta. Isso quer dizer que a energia do volume de controle aumentou?
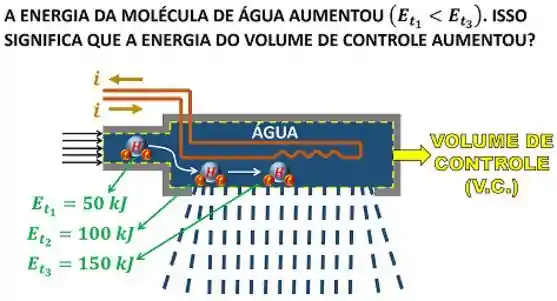
Não! Quando o processo está em regime permanente, o volume de controle é formado por pontos com propriedades constantes. Cada gotinha de água que passa pelo ponto 1, torna-se submetida às características constantes do ponto 1, e o mesmo vale para todos os outros pontos subsequentes.
Então, a energia de cada parte do volume de controle é constante. Como o volume de controle é a soma dessas partes que não mudam, sua energia total também não muda!
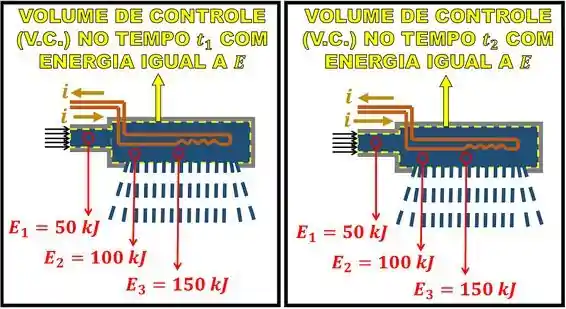
As propriedades de cada ponto em que a molécula de água está não muda, é a molécula de água que muda de ponto! Tranquilo? Então bora praticar mais alguns exercícios pra ficarmos mais craques ainda 🥳
A água fria entra no chuveiro com entalpia específica igual a e uma vazão mássica de . Se a resistência elétrica do chuveiro fornece calor para a água a uma taxa de de , quanto vale a entalpia específica da água na saída do chuveiro ? Considere que a velocidade e a altura da água que entra e sai sejam desprezíveis.
As propriedades de cada ponto do volume de controle em regime permanente são constantes
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
A figura abaixo mostra ar sendo ventilado através de uma tubulação. Suponha que o ar escoa em regime permanente pela tubulação e sofre trabalho de eixo do ventilador a uma taxa de . Considerando que o estado do ar que o estado do ar antes de ser ventilado é igual ao estado do ar depois de ser ventilado, calcule a taxa de calor trocado entre o ar e o ambiente. Despreze as variações de energia cinética e potencial do ar.
Passo 1
O enunciado pede que a gente calcule o valor da taxa de calor que o ar troca com o ambiente para conseguir voltar mesmo estado que estava antes de ser ventilado. A figura abaixo mostra todos os dados que temos para calcular o valor de .
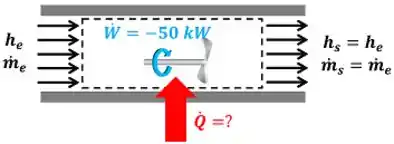
e são as vazões mássicas de entrada e saída do ar respectivamente e e são as entalpias específicas de entrada e saída do ar respectivamente. é a taxa de trabalho que o ar sofre com a ventilação. Ela é negativa, porque o ar recebe trabalho!

A entalpia de entrada é igual à entalpia de saída , porque o enunciado informa que o estado do ar que o estado do ar antes de ser ventilado é igual ao estado do ar depois de ser ventilado.

A vazão mássica de entrada é igual à vazão mássica de saída , porque o ar escoa em regime permanente. Ou seja, toda massa que entra no volume de controle (marcado pela linha pontilhada) tem que sair.
No próximo passo, veremos qual fórmula é usada para calcular .
Passo 2
Para calcular precisaremos usar a primeira lei para volumes de controle em regime permanente. Como o enunciado diz que a energia cinética e a energia potencial podem ser desprezadas, a primeira lei vira:
No entanto, as vazões e entalpias são iguais. Por causa disso:
Isso quer dizer que e podem ser cortados da fórmula. Com isso, a primeira lei se reduz a:
No próximo passo vamos substituir o valor de que temos na fórmula acima para calcular !
Passo 3
Resposta
Exercício Resolvido #2
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 262-5.115
Água líquida saturada é aquecida a uma pressão constante em um dispositivo em regime permanente até atingir o estado de vapor saturado. Calcule a transferência de calor, em , quando a vaporização é realizada a uma pressão de .
Passo 1
O enunciado pede que a gente calcule o valor da taxa de calor por unidade de massa que a água líquida saturada a recebe para se transformar totalmente em vapor saturado. A figura abaixo mostra todos os dados que temos para calcular o valor de .
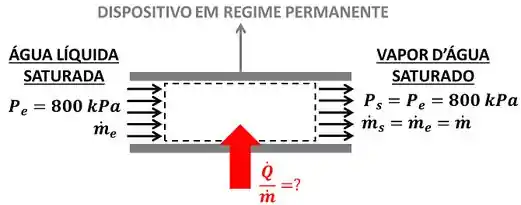
e são as vazões mássicas de entrada e saída da água respectivamente e e são as pressões de entrada e saída da água respectivamente. A vazão mássica de entrada é igual à vazão mássica de saída , porque a água escoa em regime permanente. Ou seja, toda massa que entra no volume de controle (marcado pela linha pontilhada) tem que sair.
No próximo passo, veremos qual fórmula é usada para calcular .
Passo 2
Para calcular precisaremos usar a primeira lei para volumes de controle em regime permanente. O fato do enunciado não informar nada sobre a velocidade de entrada e de saída da água e também não informar a altitude dessas vazões de água é sinal de que a questão despreza a energia cinética e a energia potencial. Levando em conta essa simplificação, a primeira lei vira:
e são as entalpias específicas de entrada e saída da água respectivamente. é a taxa de trabalho que a água realiza durante o processo de vaporização. Como o enunciado não fala nada sobre realização de trabalho de eixo pela água, é considerado nulo!
Por conta disso, a primeira lei vira:
No próximo passo vamos descobrir como encontrar o valor de e para poder calcular .
Passo 3
Podemos encontrar e em uma tabela de saturação de água como a tabela mostrada abaixo.
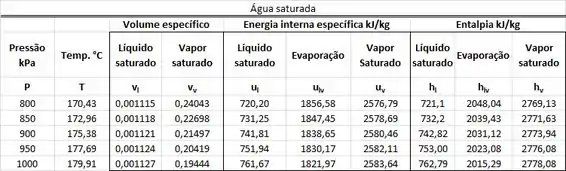
O valor de está na mesma linha que a pressão de e na mesma coluna que .
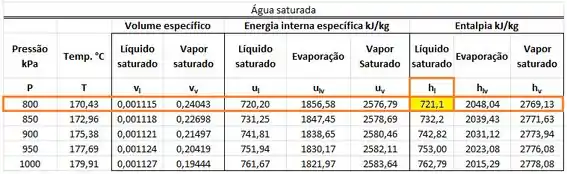
Ou seja, vale:
O valor de está na mesma linha que a pressão de e na mesma coluna que !
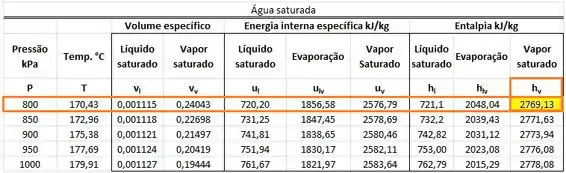
Ou seja, vale:
Agora podemos calcular .
Passo 4
Resposta
Exercício Resolvido #3
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 262-5.114
Refrigerante-134a entra no condensador de um refrigerador a e e sai como um líquido saturado à mesma pressão. Determine a transferência de calor do refrigerante por unidade de massa.
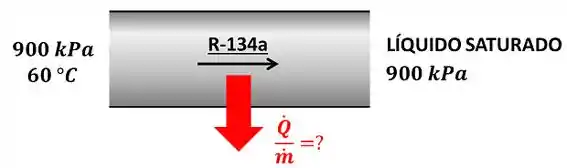
Passo 1
O enunciado pede que a gente calcule o valor da taxa de calor por unidade de massa que a refrigerante-134a a e a perde para se transformar totalmente em líquido saturado. A figura abaixo mostra todos os dados que temos para calcular o valor de .
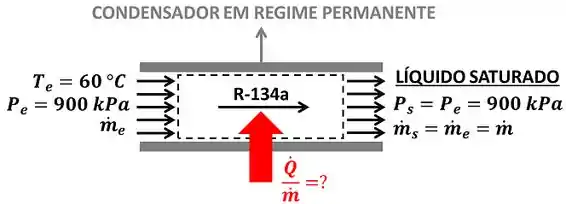
e são as vazões mássicas de entrada e saída do refrigerante-134a respectivamente e e são as pressões de entrada e saída do refrigerante-134a respectivamente. A vazão mássica de entrada é igual à vazão mássica de saída , porque o refrigerante-134a escoa em regime permanente. Ou seja, toda massa que entra no volume de controle (marcado pela linha pontilhada) tem que sair.
No próximo passo, veremos qual fórmula é usada para calcular .
Passo 2
Para calcular precisaremos usar a primeira lei para volumes de controle em regime permanente. O fato do enunciado não informar nada sobre a velocidade de entrada e de saída do refrigerante-134a e também não informar a altitude dessas vazões de refrigerante-134a é sinal de que a questão despreza a energia cinética e a energia potencial. Levando em conta essa simplificação, a primeira lei vira:
e são as entalpias específicas de entrada e saída do refrigerante-134a respectivamente. é a taxa de trabalho que o refrigerante-134a realiza durante o processo de condensação. Como o enunciado não fala nada sobre realização de trabalho de eixo pelo refrigerante-134a, é considerado nulo!
Por conta disso, a primeira lei vira:
No próximo passo vamos descobrir como encontrar o valor de e para poder calcular .
Passo 3
Podemos encontrar em uma tabela de saturação do refrigerante-134a como a tabela mostrada abaixo. O valor de está na mesma linha que a pressão de e na mesma coluna que !
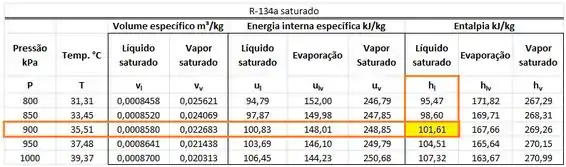
Ou seja, vale:
Podemos encontrar em uma tabela de propriedades do refrigerante-134a. A temperatura da vazão de entrada é maior que a temperatura de saturação a . Por causa disso, o R-134a entrando no condensador é um vapor superaquecido.
Por isso, achamos em uma tabela de vapor superaquecido de R-134a.
O valor de está na mesma linha que a temperatura de e na mesma coluna que .
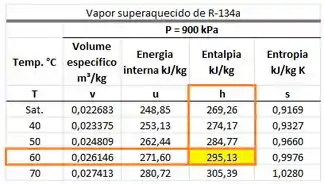
Ou seja, vale:
Agora podemos calcular .
Passo 4
Resposta
Exercício Resolvido #4
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 257-5.75
As correntes quente e fria de um fluido são misturadas em uma câmara de mistura rígida. O fluido quente flui para a câmara a uma vazão mássica de com energia de . O fluido frio flui para a câmara com uma vazão mássica de e energia de . Há transferência de calor para a vizinhança a partir da câmara de mistura a uma quantidade de . A câmara de mistura opera em regime permanente e não ganha ou perde energia ou massa com o tempo. Determine a energia transportada a partir da câmara de mistura pela mistura de fluido por unidade de massa de fluido, em .
Passo 1
Uma câmara de mistura é um equipamento que mistura duas ou mais vazões que entram nela. A figura abaixo mostra a câmara de mistura e todos os dados que o enunciado nos fornece.
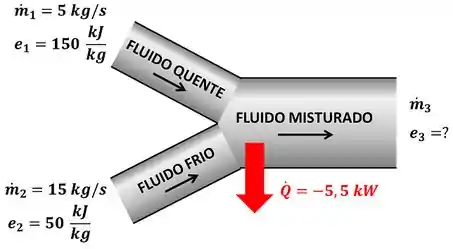
é a taxa de calor que a câmara libera para o ambiente. Ela é negativa, porque o enunciado diz que a câmara perde calor.
é a vazão mássica de fluido quente, é a vazão mássica de fluido frio e é a vazão mássica da mistura entre os fluidos quente e frio. é a energia por unidade de massa que o fluido quente carrega, é a energia por unidade de massa que o fluido frio carrega e é a energia por unidade de massa que a mistura entre os fluidos quente e frio carrega. é a incógnita do problema!

Agora vamos aprender a calcular o valor de .
Passo 2
pode ser descoberto a partir da primeira lei da termodinâmica usada em volumes de controle em regime permanente abaixo.
é a taxa de realização de trabalho do fluido.
Na fórmula acima nós vemos que a energia total por unidade de massa é a soma entre a entalpia específica , a energia cinética por unidade de massa e a energia potencial por unidade de massa . Para a gente conseguir, falta aprender a calcular e . Todos os outros termos foram dados pelo enunciado e foram mostrados pela figura.
Passo 3
Como exercício não diz em nenhum momento que o fluido realiza ou sofre trabalho de algum tipo, não existe taxa de trabalho nessa questão!
A vazão mássica da fluido misturado que está saindo as câmara é igual à soma entre as duas vazões de entrada ( e ). Essa é a fórmula de conservação de massa para volumes de controle em regime permanente.
Agora que temos todas as informações que preciamos, podemos começar os cálculos no próximo passo.
Passo 4
Iniciamos as contas encontrando o valor de .
vale:
Resposta
Exercício Resolvido #5
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 258-5.76
Uma corrente de água quente a entra em uma câmara de mistura com um fluxo de massa de , onde é misturada com uma corrente de água fria a . Para que a mistura saia da câmara a , determine o fluxo de massa da corrente de água fria. Considere que todas as correntes estão a uma pressão de .
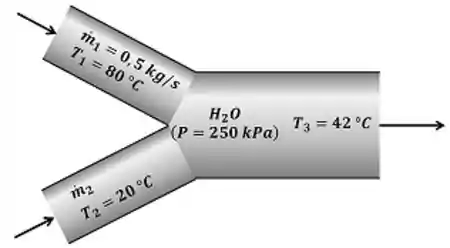
Passo 1
Uma câmara de mistura é um equipamento que mistura duas ou mais vazões que entram nele. A questão pede que a gente calcule a vazão da água . A figura abaixo mostra todos os dados que o enunciado nos informa para calcular .
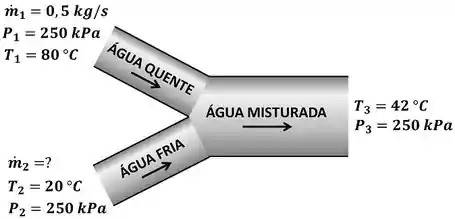
Como exercício não diz em nenhum momento que a água realiza ou sofre trabalho de algum tipo, não existe taxa de trabalho nessa questão!
O mesmo vale para ! O exercício não nos diz nada sobre troca de calor entre a água e o ambiente. Por isso, vale zero!
é a vazão mássica de água quente, é a vazão mássica de água fria e é a vazão mássica da água misturada. é a pressão e é a temperatura da água quente. é a pressão e é a temperatura da água fria. é a pressão e é a temperatura da água misturada.
Agora que entendemos o que são esses termos, vamos aprender a calcular o valor de .
Passo 2
pode ser descoberto a partir da primeira lei da termodinâmica usada em volumes de controle em regime permanente e da equação de conservação de massa. Abaixo podemos ver a primeira lei. Como o exercício não nos informa nada sobre a energia cinética e a energia potencial da água, concluímos que esses dois termos são desprezados pela questão.
é a taxa de realização de trabalho do fluido.
é a entalpia específica da água quente, é a entalpia específica da água fria e é a entalpia específica da água misturada.
pode ser caculado pela equação de conservação de massa da câmara de mistura.
Substituindo essa fórmula na primeira lei da termodinâmica, achamos:
Pra conseguir calcular só falta aprender a encontrar os valores de , e . Vamos fazer isso no próximo passo!
Passo 3
Encontramos os valores de , e a partir das tabelas de propriedades da água. O primeiro passo para decidir qual tabela usar (de saturação, de líquido comprimido ou de vapor superaquecido) é comparar as temperaturas das correntes de água (, e ) com a temperatura de saturação da água a de pressão.
Em uma tabela de saturação, vemos que a temperatura de saturação da água a vale:
Como as temperaturas (, e ) estão abaixo dessa temperatura de saturação , todas as vazões de água (quente, fria e misturada) são líquido comprimido! Por isso, temos que usar tabelas de líquido comprimido da água a . O problema é que a maioria dos livros de termodinâmica não possuem tabela de líquido comprimido para essa pressão!

No próximo passo vamos resolver esse problema!
Passo 4
Como não temos essa tabela, nós podemos considerar que a entalpia do líquido comprimido é igual à entalpia do líquido saturado na mesma temperatura! Isso quer dizer que a entalpia específica da água quente é igual à entalpia específica da água saturada à , por exemplo! Então essa entalpia está na mesma linha que e na mesma coluna que .
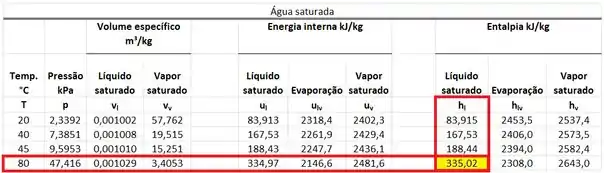
A entalpia específica da água fria está na mesma linha da temperatura de e na mesma coluna que .
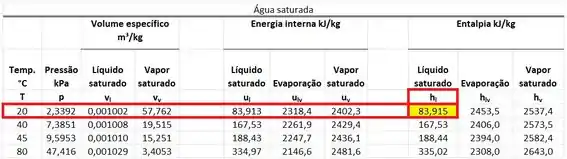
Vemos que nessa tabela não existe uma linha com de temperatura. Por isso, temos que interpolar a entalpia com as entalpias a de temperatura e a de temperatura .
Agora que temos todos esses valores podemos calcular a vazão de água fria .
Passo 5
A fórmula de se encontra abaixo.
Resposta
Exercício Resolvido #6
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 258-5.77E
Água a e é aquecida em uma câmara, misturando-a com vapor d’água saturado a . Considerando que ambos os fluxos entram na câmara de mistura com a mesma vazão mássica, determine a temeratura e o título do fluxo de saída.
Passo 1
A questão pede pra gente calcular a temperatura e o título da vazão de água que está saindo da câmara de mistura. A figura abaixo resume as informações que temos sobre o problema.
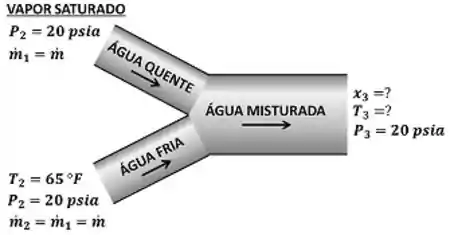
é a vazão mássica de vapor saturado d’água (água quente), é a vazão mássica de água fria e é a vazão mássica da água misturada. é a pressão e é a temperatura do vapor saturado d’água. é a pressão da água fria. é a pressão, é a temperatura e é o título da água misturada.
Agora que entendemos o que são esses termos, vamos aprender a calcular o valor de e .
Passo 2
e serão encontrados, quando a gente determinar o estado da água saindo da câmara (estado ). Para determinar o estado , precisamos encontrar o valor de duas propriedades da água nesse estado. Nós já sabemos a pressão desse estado . Ela é igual a e a , porque a pressão do fluido não varia sua pressão, quando passa pela câmara de mistura.
A entalpia específica da água misturada pode ser a segunda propriedade que precisamos para determinar o estado . Conseguimos calcular a partir da primeira lei da termodinâmica usada em volumes de controle em regime permanente e da equação de conservação de massa.

Abaixo podemos ver a primeira lei. Como o exercício não nos informa nada sobre a energia cinética e a energia potencial da água, concluímos que esses dois termos são desprezados pela questão.
Como exercício não diz em nenhum momento que a água realiza ou sofre trabalho de algum tipo, não existe taxa de trabalho nessa questão!
O mesmo vale para ! O exercício não nos diz nada sobre troca de calor entre a água e o ambiente. Por isso, vale zero!
é a entalpia específica do vapor saturado d’água, é a entalpia específica da água fria e é a entalpia específica da água misturada.
pode ser caculado pela equação de conservação de massa da câmara de mistura.
No entanto, o enunciado diz que:
Logo:
Substituindo essa informação na fórmula, achamos:
Pra conseguir calcular só falta aprender a encontrar os valores de e . Vamos fazer isso no próximo passo!
Passo 3
Como a vazão de água que se encontra no estado é uma vazão de vapor saturado, encontramos a entalpia do vapor em uma tabela de saturação da água. Nessa tabela, a entalpia se encontra na linha da pressão a e na coluna de .
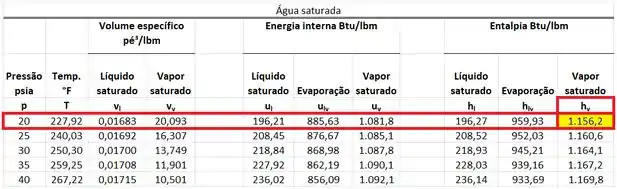
A temperatura da água mais fria está a . Isso significa que ela está a uma temperatura menor do que a temeratura de saturação na pressão de . Por conta disso, essa vazão de água que está no estado é uma vazão de líquido comprimido. Por isso, temos que usar uma tabela de água liquida comprimida para encontrar .

O problema é que a maioria dos livros de termodinâmica não possuem tabela de líquido comprimido para essa pressão!
No próximo passo resolveremos esse problema!
Passo 4
Como não temos essa tabela, nós podemos considerar que a entalpia do líquido comprimido é igual à entalpia do líquido saturado na mesma temperatura ! Isso quer dizer que a entalpia específica da água fria é igual à entalpia específica da água líquida saturada à ! Então, segundo a tabela de saturação, essa entalpia vale:
Com esse valor podemos calcular ! Mas como podemos encontrar e a partir de e ?
No passo a seguir a gente vai descobrir!
Passo 5
Se o valor da entalpia do estado estiver entre os valores de da entalpia do líquido saturado e do vapor saturado a pressão , o estado está saturado. Isso significa que é igual à temperatura de saturação da água a .
e são as entalpias específicas que estão na mesma linha que a pressão de .
Se o estado for saturado, calculamos o seu título pela fórmula abaixo.
Agora que sabemos de tudo isso, vamos começar os cálculos!
Passo 6
Iniciamos as contas, determinando o valor de .
Como esse valor está entre e , o estado está saturado. Por isso, sua temperatura é igual à temperatura de saturação .
Descobrimos o valor de a partir da sua fórmula.
Resposta
Exercício Resolvido #7
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 261-5.111
Uma casa tem um sistema de aquecimento elétrico que consiste em um ventilador de e um resistor colocado em um duto. O ar escoa em regime permanente no duto com vazão igual a e sofre um aumento de temperatura de . A taxa de perda de calor do duto é estimada em . Determine a potência nominal do sistema de aquecimento elétrico.
Passo 1
A questão pede para a gente calcular a potência nominal do sistema de aquecimento elétrico. Isso significa que precisamos calcular a taxa de trabalho elétrico que a resistência elétrica realiza sobre o ar do duto . A figua abaixo mostra todos os dados que temos para calcular .
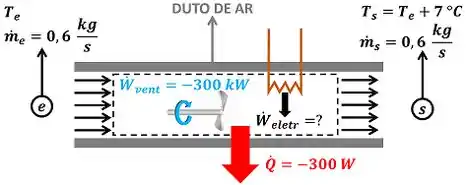
é a temperatura e é a vazão mássica de ar entrando no volume de controle. é a temperatura e é a vazão mássica de ar saindo no volume de controle. é a taxa de trabalho que o ventilador realiza sobre o ar. Ele é negativo, porque o ar está recebendo energia.
é a taxa de calor que o duto perde . Como o calor está saindo do duto, também é negativo.
Agora que sabemos o que cada termo da figura significa, vamos descobrir como calcular no próximo passo.
Passo 2
Conseguimos calcular a partir da primeira lei da termodinâmica usada em volumes de controle em regime permanente. Abaixo podemos ver a primeira lei. Como o exercício não nos informa nada sobre a energia cinética e a energia potencial da água, concluímos que esses dois termos são desprezados pela questão.
e são as entalpias específicas do ar entrando no duto e do ar saindo do duto respectivamente.
Atenção é a soma de todas as taxas de trabalho que entram e saem do volume de controle. Logo, seu valor pode ser calculado pela fórmula abaixo.
Substituindo essa fórmula na primeira lei, achamos uma fórmula para .
Como as duas vazões mássicas e são iguais, podemos reescrever a fórmula acima.
Ou seja, para calcular só falta aprender a calcular . No próximo passo aprenderemos a calcular !
Passo 3
Se considerarmos o ar como um gás perfeito que possui calor específico a pressão constante com valor constante, pode ser calculado com a fórmula abaixo.
onde o do ar vale:
Agora que já sabemos fazer esse cálculo, vamos começar as contas.
Passo 4
A primeira conta que precisamos fazer é para descobrir quanto vale .
Agora podemos achar o valor de . Antes de fazer isso, precisamos converter os valores de e que estão em watt para valores em quilowatt .
Resposta
Exercício Resolvido #8
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 262-5.116
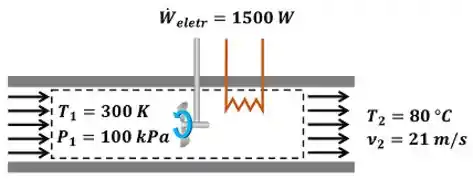
Ar a e flui em regime permanente em um secador de cabelo que consome . Por causa do tamanho da entrada de ar, a velocidade do ar na entrada é desprezível. A temperatura do ar e a velocidade na saída do secador de cabelo correspondem a e respectivamente. O escoamento do ar ocorre a uma pressão constante e de forma adiabática. Considere que o ar possui calores especifícos constantes de . Determine a vazão mássica de ar no secador de cabelo, em . Determine a vazão volumétrica de ar na saída do secador de cabelo, em .
Passo 1
O exercício pede para a gente calcular a vazão mássica de ar que passa pelo secador de cabelo. A figura abaixo mostra todos as informações dadas pelo enunciado para calcular .
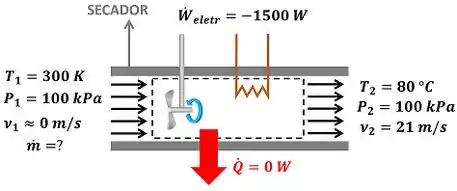
é a temperatura, é a pressão, é a velocidade do ar que está entrando no secador. é a temperatura, é a pressão, é a velocidade do ar que está saindo do secador. é a potência elétrica (taxa de trabalho elétrico) que o secador consome. Diferente da imagem do enunciado, ela é considerada negativa na resolução da questão, porque a energia está entrando no ar que passa pelo volume de controle.
A figura só mostra o valor de positivo, porque ela está mostrando apenas o módulo de .
Além disso, a questão diz que e escoamento de ar é adiabático. Isso significa que o ar não ganha nem perde calor. Ou sexa, a taxa de troca de calor entre o ar e o ambiente é nula!
Outro dado importante do enunciado é que ele diz que o escoamento do ar ocorre a pressão constante. Isso quer dizer que a pressão de entrada do ar é igual à pressão de saída do ar .
Com essas informações, podemos aprender a calcular a vazão mássica de ar .
Passo 2
pode ser calculada a partir da primeira lei da termodinâmica usada em volumes de controle em regime permanente. Como o exercício não nos informa nada sobre a energia potencial da água, concluímos que esse termo é desprezado pela questão. A energia cinética do ar entrando no secador é admitida nula, porque o enunciado diz que a velocidade de entrada é desprezível. A forma da primeira lei com todas essas considerações está abaixo.
Reorganizando a primeira lei, achamos uma fórmula para .
Ou seja, para calcular só falta aprender a calcular . No próximo passo aprenderemos a calcular !
Passo 3
Se considerarmos o ar como um gás perfeito que possui calor específico a pressão constante com valor constante, pode ser calculado com a fórmula abaixo.
onde o do ar vale:
Agora que já sabemos fazer esse cálculo, vamos começar as contas.
Passo 4
A primeira conta que precisamos fazer é para descobrir quanto vale . Para fazer esse cálculo, precisamos primeiro converter a temperatura de grau Celsius para kelvin .
Agora podemos achar o valor de . Antes de fazer isso, precisamos converter os valores de e que estão em watt para valores em quilowatt .
Além disso, é necessário dividir o termo de energia cinética do ar que está saindo do secador por mil. Isso faz o termo passar de para .
Vamos aprender no próximo passo como calcular a vazão volumétrica de saída do ar .
Passo 5
Podemos calcular a partir de , dividindo pela massa específica do ar que sai do secador .
pode ser calculado a partir da equação de gás de perfeito aplicada ao ar saindo do secador.
onde é o volume específico do ar saindo do secador e é a constante de gás do ar. Ela vale:
Agora que temos todos esses dados, vamos calcular .
Passo 6
O primeiro passo para esse cálculo é achar .
Agora podemos encontrar .