Na indústria cerâmica, avalia-se sistematicamente a resistência de amostras de massas cerâmicas, após o processo de queima. Dessas avaliações, sabe-se que certo tipo de massa tem resistência mecânica aproximadamente normal, com média e variância Após a troca de alguns fornecedores de matérias- primas, deseja-se verificar se houve alteração na qualidade. Uma amostra de corpos de prova de massa cerâmica acusou média igual a . Qual é a conclusão ao nível de significância de ?
Passo 1
Queremos testar se houve alteração na qualidade, ou seja, se a média é diferente de . Então nossa hipótese nula vai ser:
Nada foi dito se é maior ou menor que isso, então usamos só o mesmo.
E a alternativa, é justamente o que queremos testar:
Então estamos num teste bilateral.
Passo 2
No bilateral, nossa estatística de teste é dada por:
No nosso caso, substituindo os valores do enunciado, ficamos com:
Lembrando que o foi dado foi a variância que vale , então o é a raiz disso, ou seja, .
Passo 3
No bilateral, nossos pontos críticos são:
É pedido um nível de significância de , então:
Portanto:
Então nossa região crítica fica sendo:
Passo 4
Então desenhando nossa região crítica e vendo a localização da nossa estatística de teste:
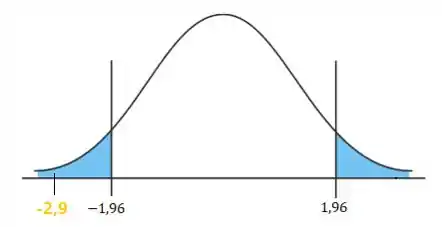
Vemos que ela cai dentro da , ou seja, rejeitamos a hipótese nula!