Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Transformada inversa de s^n

Ver Teoria
Exercício 2134

Enunciado

Calcule

L - 1 s 3 + 2 s 2 + 6 s + 5 s + 1

Passo 1

Beleza, olha só. Pra questões desse tipo, com polinômios sobre polinômios, as chances de dar pra simplificar são enormes. Sendo assim, vamos olhar pro denominador que é mais simples. Veja que se s = - 1 , então o denominador assume o valor s + 1 = 0 . O que será que acontece com o numerador usando o mesmo s ?

s 3 + 2 s 2 + 6 s + 5 =

= - 1 3 + 2 . - 1 2 + 6 - 1 + 5 =

= - 1 + 2 - 6 + 5 = 1 - 1 = 0

Opa, então - 1 é uma raiz do polinômio no numerador.

Passo 2

Você pode estar se perguntando: como isso ajuda a gente? Bem, veja só, se sabemos uma raiz do polinômio, podemos dividir ele usando Briot Ruffini (BR). Montando a matriz BR temos:

Descemos o número 1 e multiplicamos ele pela raiz conhecida, somando ao próximo número. O resultado dessa conta, a gente põe logo a baixo:

1 ∙ - 1 + 2 = 1

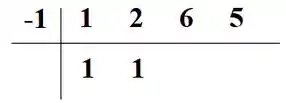
Repetimos o processo pro 1 recém escrito, somando dessa vez com o próximo número na parte de cima, isto é, o número 6 :

1 ∙ - 1 + 6 = 5

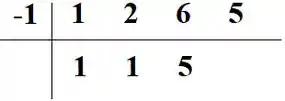
E pra fechar, fazemos uma última vez seguindo a mesma ideia

5 ∙ - 1 + 5 = 0

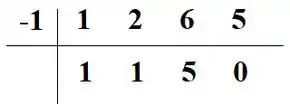
Sendo o último número o resto R = 0 , r = - 1 a raiz conhecida do polinômio do numerador, a matriz BR nos revela que podemos reescrever o polinômio para:

s 3 + 2 s 2 + 6 s + 5 = s - r s 2 + s + 5 + R

s 3 + 2 s 2 + 6 s + 5 = s + 1 s 2 + s + 5

Passo 3

Na verdade pessoal, a gente feshow essa questão já! Veja só, usando a simplificação que calculamos no passo anterior:

L - 1 s 3 + 2 s 2 + 6 s + 5 s + 1 = L - 1 s + 1 s 2 + s + 5 s + 1 = L - 1 s 2 + s + 5

L - 1 s 2 + s + 5 = δ ' ' t + δ ' t + 5 ∙ δ t

Resposta

L - 1 s 3 + 2 s 2 + 6 s + 5 s + 1 = δ ' ' t + δ ' t + 5 ∙ δ t