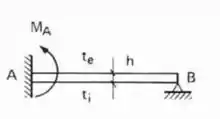
Para estrutura abaixo, sabendo que à mesma possui a temperatura das fibras externas igual a e a temperatura das fibras internas igual a , determine a deformação horizontal do ponto C.
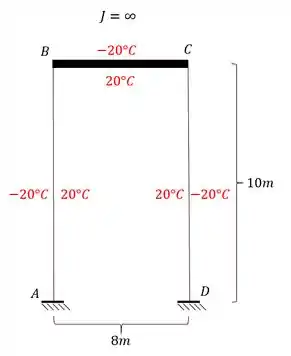
Passo 1
Antes de tudo precisamos saber a temperatura no da nossa estrutura, sabemos que se for diferente de zero, deveremos usar williot, se for igual a zero, teremos que usar as formulazinhas básicas que temos.
Com isso, basta desenharmos o nosso diagrama de temperatura, e vermos no que vai dar, sendo assim teremos que:
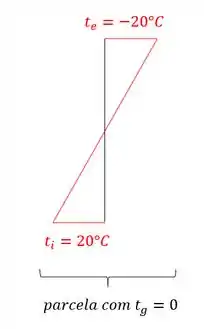
Com isso vemos que a nossa estrutura tem a temperatura no centro de gravidade igual a zero.
Logo as fórmulas que temos que usar são:
- Caso Bi-engastado
- Caso Engastado e apoiado
- Analisando primeiro as deslocabilidades internas:
- Sabemos que os pontos A e D são indeslocáveis, logo, não possuem deslocabilidade interna.
- Agora que vem o diferencial. Os pontos C e B estão nas extremidades da barra com inércia infinita. SEMPRE que tivermos uma barra com inércia infinita, ela obrigatoriamente tornará os nós da sua extremidade indeslocaveis com relação a rotação. Ou seja, os nós C e B não podem rotacionar porque a barra CB possui uma inércia tão grande que já vai impedir isso. Ou seja, não temos deslocabilidade interna.
- Analisando agora as deslocabilidades externas:
- Os pontos A e D são engastes, logo são considerados indeslocaveis.
- O ponto C também não pode se deslocar na vertical, porém pode claramente se deslocar na horizontal, por isso devemos travar ele nesse sentido, com o nosso velho amigo apoio do primeiro gênero.
- Com o ponto C travado podemos ver que passamos a ter o ponto B indeslocavel, logo teremos apenas 1 deslocabilidade externa mesmo.
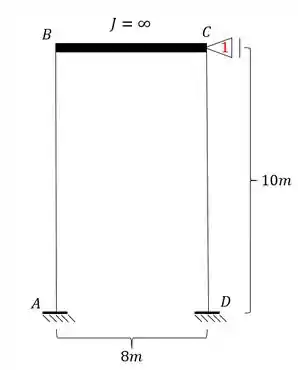
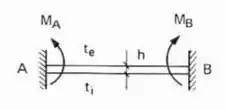
- Caso Bi-engastado
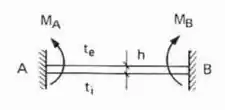
E pasmem, é só isso mesmo que fazemos quando o .
Mas ainda tem uma observação muito importante:
Os sinais dos momentos são feitos levando em consideração que , ou seja, que as temperaturas das fibras internas são maiores que as da externa.
E no nosso caso é exatamente isso que acontece, então podemos ficar tranquilos quanto a isso.
Passo 2
Sabendo qual é o nosso caso, precisamos agora definir as nossas deslocabilidades.
Passo 3
Determinado tudo isso vamos definir o valor de .
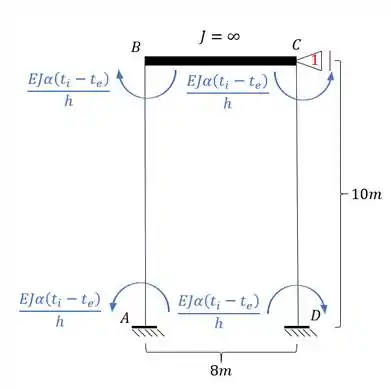
Perceba que todas as barras ou possuem na sua extremidade, ou um engaste ou uma barra de inércia infinita que sabemos que impede rotação. Dessa maneira a nossa estrutura pode ser definida como um tipo de estrutura Bi-engastada.
E aplicando isso a nossa estrutura teremos que:
Substituindo os valores teremos que:
E para determinarmos teremos que determinar a reação de apoio que receberá contribuição apenas das barras AB e CD.
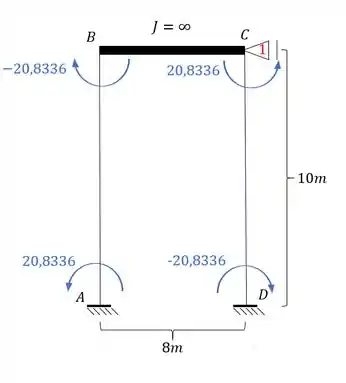
Calculando as reações teremos que:
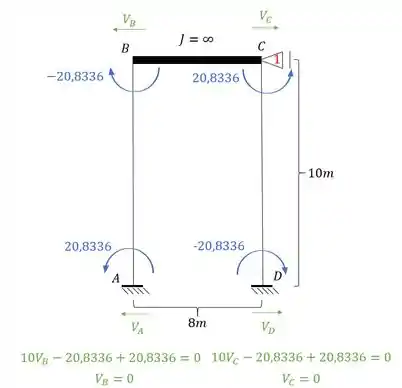
Perceba que temos duas reações de apoio, e que elas deram pra baixo (que é o nosso sentido negativo), dessa maneira teremos que:
Passo 2
Agora que definimos as rigidezes do sistema zero, precisamos determinar nos sistemas com a deformação de cada um dos travamentos, sendo assim teremos que:
Para determinar o valor é muito simples, é só determinarmos a reação de apoio que age no nosso ponto 1.
Como temos que deslocar o nosso apoio em 1, e sabemos que todos os nossos nós são engastes, usaremos a seguinte fórmula:
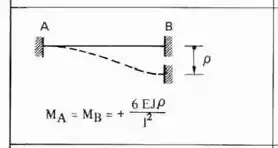
Colocando o deslocamento na nossa estrutura teremos que:
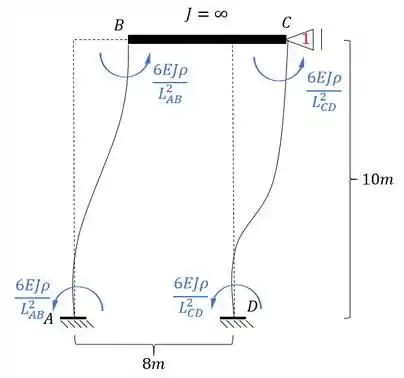
Usando o fator de rigidez relativa teremos que:
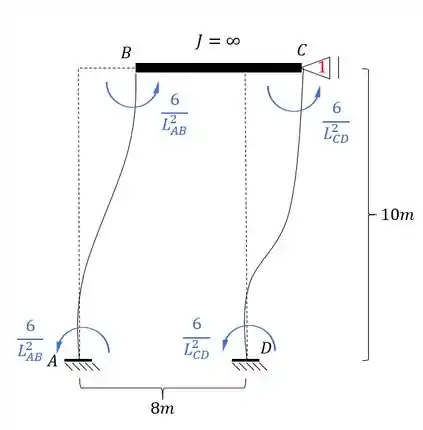
Como todos os comprimentos são iguais teremos que:
Veja que somente as barras AB e DC produziram reações na horizontal, por isso iremos calcular apenas a reação de apoio referente a elas, sendo assim teremos que:
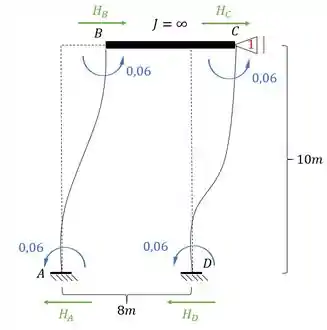
E aqui temos uma diferença importante, o sentido da reação nesse caso, é o mesmo da força calculada, ou seja, se e estão pra frente, e na mesma direção do apoio 1, então a reação em 1 vai ser pra frente também e com o mesmo valor de . Sendo assim teremos que:
Passo 3
Resolvendo o nosso sistema vamos ter que:
Substituindo teremos que:
Nosso objetivo era determinar a deformação horizontal do ponto B, que é exatamente o ponto que colocamos o apoio do primeiro gênero 1, que nós da o .
Vale lembrar que também dividimos tudo por EJ, ou seja, precisamos dividir aqui para termos o resultado real.
Ou seja, pela simetria da estrutura e do carregamento de temperatura, o ponto B não sofre deslocamentos.