Um banhista precisa cruzar uma certa faixa de areia na praia, partindo do ponto A em direção ao acampamento no ponto B. Ele pode fazer isso atravessando perpendicularmente a faixa de areia e andando o restante ao longo de uma trilha ou cruzando-a em um ângulo , até um certo ponto, e andando o restante ao longo da trilha:
Considerando-se que o banhista caminha a na areia e a na trilha, determine o tempo para que ele chegue ao acampamento para diversos valores de
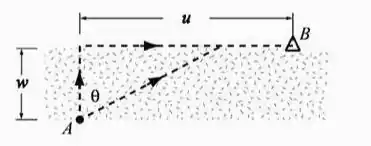
As distâncias do ponto A até a trilha perpendicularmente (w) é e a distância do inicio da trilha até o ponto B(u) é
Escreva um programa em uma rotina para resolver o problema.
Passo 1
Opa pessoal esse exercício é uma combinação de 2 conteúdos.
Que é o conteúdo de funções para otimizar o nosso procedimento de cálculo, mas também é um conteúdo que envolve testes lógicos pois temos duas condições.
Qual condição aplicar depende de onde o banhista chega, por exemplo se ele for em um ângulo onde seu ponto final é antes do ponto , ele será obrigado a andar pela trilha modificando assim sua velocidade.
Mas primeiramente vamos equacionar o problema, como o ângulo e é fixo vamos utilizar a equação da tangente.
Logo:
Analisando a figura
Agora podemos calcular o valor de a partir dos dados do problema e se ele for menor do que os 14 km o nosso banhista precisa andar a diferença na trilha, sacou?
Agora que já equacionamos o problema vamos montar nossa
Passo 2
Para criar a precisamos primeiro lembrar da sua sintaxe.
A sintaxe da é a seguinte:
Primeiramente vamos anexar ela a alguma variável, pode ser qualquer letra ou nome, desde que não detenha caracteres especiais.
E depois vamos dar um nome para ela, nessa questão eu vou chamar de forma arbitrária a variável de e dar o nome de
Então minha fica:
Agora precisamos inserir as variáveis que vai alimentar nossa função, a questão nos dá o ângulo em graus e vou chamar esse valor de , sendo assim a function é:
Vamos lá, agora que já iniciamos a function vamos criar seus elementos, lembre-se que queremos que a saída dessa função seja apenas o tempo de caminhada.
Primeiramente, vamos inserir a função para converter os graus em radianos junto com nosso valor de w.
Após isso vamos inserir a equação para calcular o valor de u, resultando:

Agora que temos como calcular o vamos inserir nosso teste lógico, que corresponde ao seguinte:
Se o valor de for menor que 14 é maior do que 0 temos que o tampo do percurso é a soma do tempo da areia mais o tempo da trilha resultando em:
Caso contrário é apenas:
Pois todo o trajeto foi pela areia e a menor distância é dada por uma reta que liga os dois pontos, por teorema de Pitágoras a distância é dada por:
Implementado no Matlab temos:

E para finalizar vamos colocar uma saída de dados para imprimir o tempo mais organizado:
A sintaxe da função é a seguinte:
![]()
Onde devemos chamar a função, abrir um parêntese e escrever o texto que desejamos entre aspas simples.
No lugar que queremos imprimir os valores devemos colocar pois nossa variável geralmente é flutuante pois nem sempre toda raiz sai um número inteiro.
Após realizar essa operação, antes de fechar os parênteses da função devemos linkar os a cada variável.
No caso vamos linkar o a variável f que é o tempo.
Sendo assim, o código se torna:
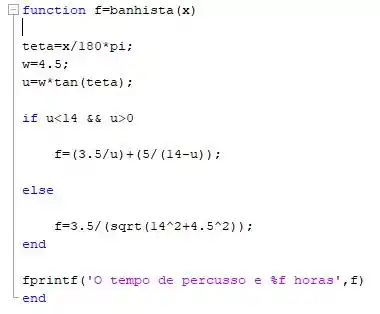
Passo 3
Indo no janela de command Windows e executando a seguinte linha de código:
Irá mostrar a seguinte informação:
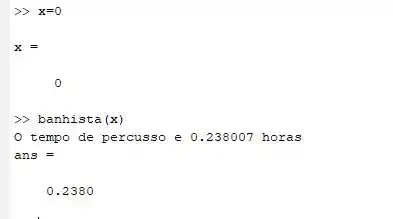
Mostrando que conseguimos finalizar o problema.
Resposta
Ei, a resposta está no passo a passo :)