Imagine duas partículas idênticas imersas em um mesmo fluido estagnado. Sem nada pra fazer, as duas partículas resolveram apostar corrida. Sabendo que as partículas estão expostas a campo de força centrífugo apenas e cada uma está exposta a um campo de mesma direção e sentido, mas intensidades diferentes, qual das duas partículas ganhará a corrida?
Despreze a fase acelerada do movimento e considere que o coeficiente de arrasto é igual para as duas partículas.
Passo 1
Que louco! Duas partículas disputando corrida haha Mas deixa elas lá né, fazer o que? Haha
Bora focar no que interessa: quem ganhará a corrida? O enunciado manda desprezar a fase acelerada do movimento, daí, consideramos que, desde o início, partículas caminham com velocidade terminal. Como vimos lá na teoria, a expressão pra velocidade terminal em fluido estagnado é:
Agora, temos duas partículas, então vamos ter que comparar as velocidades delas. A que tiver maior velocidade, ganhará a corrida.
Passo 2
Olhando, novamente, pra expressão da velocidade terminal:
Bora destacar, em vermelho, tudo que for igual nas duas partículas:
- Partículas são idênticas, daí iguais e
- Enunciado fala pra considerar iguais coeficientes de arrasto, isto é,
- Como o fluido é o mesmo, iguais
Daí:
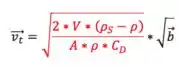
Ou seja, nessas condições, a diferença de velocidade depende apenas do campo. Quem tiver maior campo terá maior velocidade terminal e ganhará a corrida.
Resposta
Nessas condições, a diferença de velocidade depende apenas do campo. Quem tiver maior campo terá maior velocidade terminal e ganhará a corrida.