Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Aceleração Média

Ver Teoria
Exercício 1712345678910111213141516181920

Enunciado

Tipler, Mosca; Física Para Cientistas e Engenheiros; 6ª Ed. - Capítulo 2, Seção 1, Questão 60.

(Cap 2 – Ex 60) Uma partícula se move ao longo do eixo x com a velocidade v x = ( 8,0   m / s 2 ) ⋅ t - 7,0   m / s . (a) Encontre a aceleração média para dois diferentes intervalos de um segundo, um começando em t = 3,0   s e outro começando em t = 4,0   s . Esboce v x   v e r s u s   t para o intervalo 0 < t < 10   s . (c) Compare as acelerações instantâneas no meio de cada um dos dois intervalos de tempo especificados na Parte (a) com as acelerações médias encontradas na Parte (a) e comente.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

  1. A aceleração média é definida como, a mudança de velocidade em função do tempo e é dada por:

    2. a m é d = ∆ v ∆ t

    Logo, nossa aceleração média será:

    a m é d = v 2 - v 1 t 2 - t 1

    Vamos então encontrar os valores de v x para os 3, 4 e 5 s.

    v x = ( 8,0   m / s 2 ) ⋅ t - 7,0   m / s

    v x ( 3   s ) = ( 8,0   m / s 2 ) ⋅ 3   s - 7,0   m / s

    v x 3   s = 17 m / s

    v x ( 4   s ) = ( 8,0   m / s 2 ) ⋅ 4   s - 7,0   m / s

    v x 4   s = 25   m / s

    v x ( 5   s ) = ( 8,0   m / s 2 ) ⋅ 5   s - 7,0   m / s

    v x 5   s = 33   m / s

    A nossa aceleração de 3 para 4 segundos é de:

    a m é d = v x 4   s - v x 3   s 4   s - 3   s

    a m é d = 25   m / s - 17 m / s 4   s - 3   s

    a m é d = 8   m / s 2

    A nossa aceleração de 4 para 5 segundos é de:

    a m é d = v x 5   s - v x 4   s 5   s - 4   s

    a m é d = 33   m / s - 25 m / s 5   s - 4   s

    a m é d = 8   m / s 2

    Passo 2

  2. Temos os dados que pudemos obter no passo anterior para poder construir o gráfico

x x = - 7   m / s                 1   m / s                   9 m / s                       17 m / s

t =                         0                                       1 s                                     2 s                                         3 s                        

O gráfico de v x   v e r s u s   t é dado por:

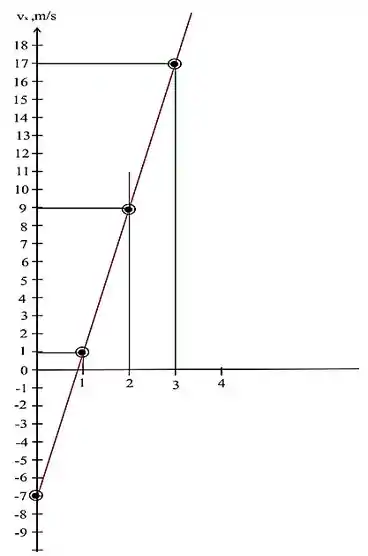
Passo 2

A aceleração instantânea é definida como a derivada temporal da velocidade:

a x = d v x d t = d d t [ ( 8,0   m / s 2 ) ⋅ t - 7,0   m / s ]

a x = 8,0   m / s 2

Podemos então inferir que, o fato de a velocidade da partícula variar linearmente com o tempo, faz com que suas acelerações sejam as mesmas.

Resposta

a ) a m é d = 8   m / s 2

c )   A s   a c e l e r a ç õ e s   s ã o   a s   m e s m a s   p o i s   a   v e l o c i d a d e   v a r i a   l i n e a r m e n t e   c o m   o   t e m p o .

Exercícios de Livros Relacionados

Em um certo instante de tempo, uma partícula tinha uma velocidadede 18m / s no sentido positivo de x ; 2,4s depois, a velocidade era 30m / s no sentido oposto. Qual foi a aceleração média da partícula
Quando nós resolvemos problemas de queda livre perto da Terra, é importante lembrar que a resistência do ar pode ter um papel importante. Se os seus efeitos são significativos, nós podemos achar respo
Você está dirigindo um carro no limite de rapidez de 25m i / h , quando você observa um sinal na interseção a 65m de você ficar amarelo. Você sabe que, naquela interseção em particular, o sinal fica a
Uma partícula se move ao longo do eixo x com a velocidade v x = ( 8,0m / s 2 ) ⋅ t - 7,0m / s . (a) Encontre a aceleração média para dois diferentes intervalos de um segundo, um começando em t = 3,0s
Calcule a velocidade e a aceleração de um corpo situado na linha do equador, decorrentes do movimento de rotação da Terra, considerando que a circunferência desta vale 40000k m .