Cônicas com Rotação – Método dos Autovalores
Produzido por Aline BuzziTeoria
Introdução
Você provavelmente conhece curvas famosos como parábolas, elipses e hipérboles quando elas estão retinhas ao longo do eixo ou . Mas acredite: existem cônicas que estão tortas, tipo essa parábola:
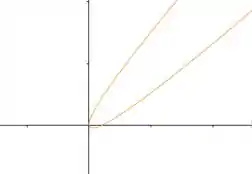
Chamamos essas cônicas de rotacionadas. Normalmente o exercício dá a equação geral delas e precisamos descobrir qual cônica é.
Existem duas maneiras de fazer isso: o método matricial (mais usado em geometria analítica) e o método dos autovalores (mais usado em álgebra linear), que é o que vamos ver agora :)
Equação Geral das Cônica
Normalmente, nesses exercícios, vamos ter uma equação no formato geral, que é assim:
Sendo que e são constantes.
Lembrando: qualquer cônica pode ser escrita com essa equação geral.
Cônicas Degeneradas
Olhando a expressão podemos nos perguntar: só existe as cônicas parábola, elipse e hipérbole??
![]()
Relaxa!! Vamos te mostrar que além dessas três que já conhecemos, existem também as cônicas que chamamos de cônicas degeneradas.
As cônicas degeneradas são todas as outras cônicas que não são elipse, parábola ou hipérbole. Alguns exemplos são:
- (vazio)
- (circunferência)
- (, eixo )
- (par de retas, os eixos e )
- (origem)
- (par de retas paralelas)
- (reta)
Voltando para as cônicas não degeneradas, ou seja, elipse, parábola e hipérbole.
Na equação geral que vimos acima vemos que a equação tem um termo . Por meio desses termo temos dois casos:
- Caso 1: , se isso ocorre, então significa que a cônica pode estar no máximo transladada, igual os casos que já vimos nos assuntos anteriores
- Caso 2: , significa que a cônica está rotacionada. Além disso, ela pode estar transladada também viu?
Cônicas com rotação
Vamos te ensinar um método de resolução para o CASO 2 em que utilizaremos vários conceitos da álgebra linear e geometria analítica. Mas, não se desespere!! Vamos te ensinar de uma forma prática, para que você entenda o método de resolução, blz?!

Para rotacionarmos cônicas, vamos tirar ela do sistema de coordenadas e passar pro sistema .
Primeiro, vamos relembrar a forma genérica de uma cônicas que vimos antes:
Guarde essa expressão com carinho!!
Pra entendermos direitinho, vamos supor que o exercício nos deu a equação:
Os nossos coeficientes são: , , , , e .
Como nesse caso , ou seja, como temos o termo , a cônica está rotacionada, então bora lá ajustar essa equação e descobrir que cônica é essa.
Passo 1 - Escrevendo de forma matricial
Aquela equação geral de cônicas, pode ser reescrita de forma matricial:
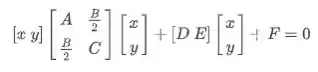
Acredite em mim, se fizermos as multiplicações de matrizes direitinho, obteremos a mesma expressão
Vamos utilizar essa expressão no exemplo anterior. E outro detalhe, quando for montar as matrizes se atente para o local exato das constantes, ou seja, a constante é a do a do e assim por diante.
Então, no nosso exemplo:
Passo 2 – Encontrando a matriz H
Montada a expressão vamos definir a matriz que chamaremos de matriz .
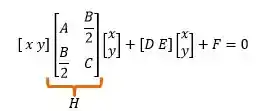
Então, no nosso caso:
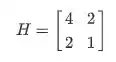
Passo 3 – Calculando os autovalores
Tendo a matriz acharemos os autovalores dessa matriz!! Mas, o que são autovalores?

Calma!!!
Relembrando, vimos que autovalores de uma matriz A são os valores que pode assumir na equação:
(3)
Vamos calcular os autovalores da nossa matriz para exemplificar:
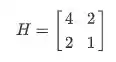
Pra calcular os autovalores, vamos calcular, ou seja, a matriz menos a matriz identidade multiplicada por:
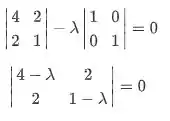
Calculando o determinante dessa matriz, temos:
Os valores de são:
O que chamamos de AUTOVALORES são os que encontramos.
Passo 4 – Calculando os autovetores unitários
Já que temos os autovalores vamos encontrar agora os AUTOVETORES!! Para cada autovalor temos um autovetor!! Além disso, o autovetor que encontrarmos deve ser unitário, ou seja, seu módulo deve ser 1!!
Muita informação!! Vamos com calma!!
Então, supondo que nosso autovetor é:
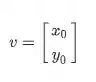
Acharemos os valores de e fazendo simplesmente:
No nosso exemplo:
- Para
Vamos começar achando o autovetor para . Teremos:
Como a matriz identidade fica anulada pelo 0:
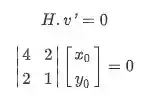
Encontramos nesse caso duas equações:
Note que a primeira equação é o dobro da segunda. Podemos isolar na segunda equação::
Vamos atribuir valores agora. Se escolhermos , será .
Encontramos o autovetor então? Quase, calma aí!! Estamos esquecendo que ele deve ser unitário!! Então, devemos calcular o módulo do autovetor e dividir cada uma das suas coordenadas pelo módulo.
Temos que , seu módulo é . Portanto, nosso autovetor unitário, será:
- Para
Agora vamos calcular o autovetor para , o esquema é o mesmo:
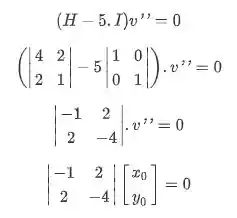
Montando a expressão multiplicando a partir da primeira linha, temos:
Atribuindo valores novamente e escolhendo , temos que . Agora vamos deixar esse vetor unitário.
Tendo , seu módulo vai ser , logo, o nosso vetor unitário vai ser
Passo 5 – Montando as matrizes D e P
Tendo os autovalores e autovetores unitário, montaremos duas matrizes: A matriz que será a matriz de autovetores e a matriz que será a matriz de autovalores. Essas matrizes são montadas da seguinte forma:
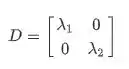
Então, para montar a matriz você colocará na sua diagonal os valores que você encontrou para os autovalores e na diagonal secundária será sempre ZEROS.
Já na matriz , suas colunas serão referentes a um dos autovetores. Por exemplo, se considerarmos o autovetor e o segundo autovetor então, nossa matriz será:
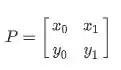
Temos que tomar um cuidado!! A primeira coluna da matriz deve possui o autovetor relacionado ao mesmo autovalor que está na coluna 1 da matriz , e na segunda coluna a mesma coisa. Então, teremos a seguinte ligação;
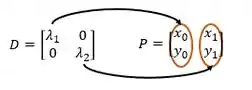
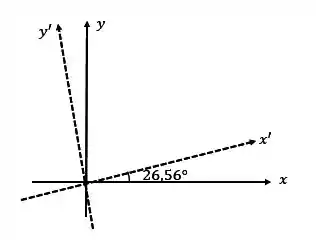
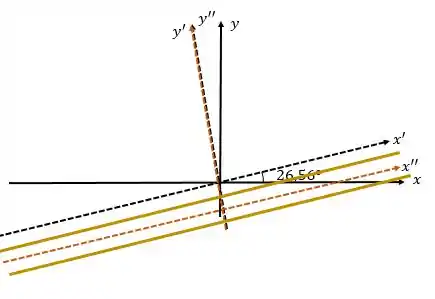
A matriz tem ainda uma outra característica!! Ela que dá o ângulo de rotação da nossa cônica, pois:
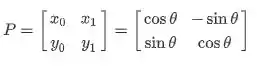
Assim, a rotação da nossa cônica será .
No nosso exemplo:
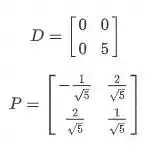
Passo 6 – Escrevendo a expressão
Tendo calculado todos os passos anteriores, vamos usar as informações que encontramos para escrever a seguinte expressão:
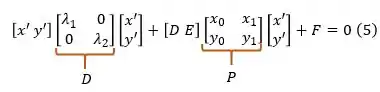
Nesse ponto conseguimos ver que todos os cálculos que fizemos anteriormente serviram para fazer uma mudança de coordenadas de para . Isso foi feito para eliminar o termo da cônica e conseguirmos então trabalhar com ela.
Tendo a expressão acima, vamos fazer as multiplicações das matrizes e então chegaremos numa equação que dependerá de e e voltaremos aos problemas do Tópico 1, onde passaremos a ter o termo , ou seja, bastará completarmos quadrados para encontrar a cônica. Então, no nosso exemplo:
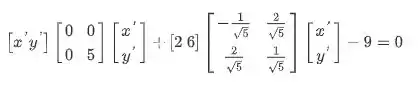
Multiplicando as matrizes:
Oba!! Agora temos nossa equação no novo sistema de coordenadas e sem o termo :D agora sim bora descobrir que cônica é essa!
Completando quadrados em :
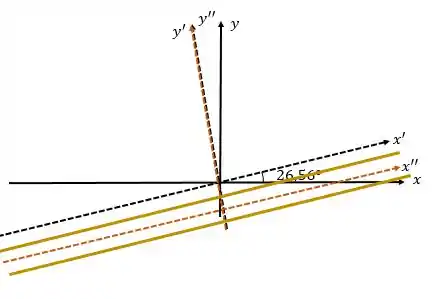
Fazendo os ajustes necessários, teremos que isso é uma parábola transladada ao longo do eixo . Abaixo temos o esboço dessa parábola antes de ser rotacionada (em azul) e depois de fazermos todos esses ajustes (em vermelho):
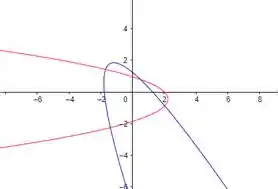
No tópico 1, quando falamos de translação de cônicas também fizemos uma mudança de coordenadas e para isso tínhamos uma relação entre e , e nesse caso qual a relação entre e . Neste, caso a relação é a seguinte:
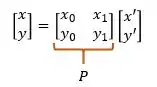
Ufa!!! Agora sim, você já sabe tudo o que você precisa para resolver esse tipo de problema!!

Para finalizar nosso estudo sobre cônicas, vamos falar um pouco sobre a representação paramétrica de alguma das cônicas!!
Equações Paramétricas da Cônicas
Das várias cônicas que existem, 3 delas possuem equações paramétricas. Mas o que são equações paramétricas?
É uma forma diferente de representar as cônicas, em geral utilizando coordenadas polares para as cônicas, pois são .
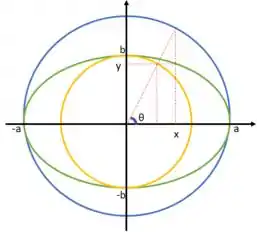
- Elipse
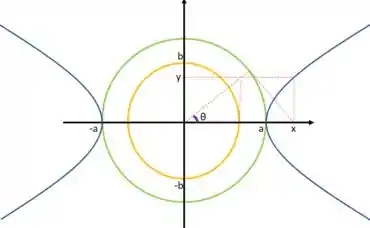
- Hipérbole
- Circunferência
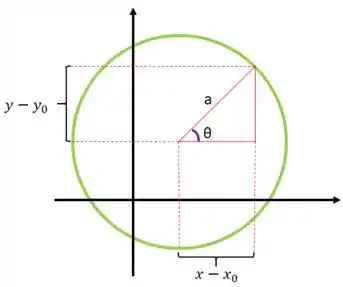
Considerando uma elipse com equação:
Podemos observar na figura abaixo que teremos como equações paramétricas:
Considerando uma hipérbole com equação:
Com a ajuda de algumas relações trigonométricas simples e da figura abaixo, obteremos como equações paramétricas:
Considerando uma circunferência, como mostra a figura abaixo, com equação:
Teremos como equações paramétricas:
Agora sim, acabouuuu!! Uhulll
Bora praticar com os exercícios?!

Cônicas com rotação
Equações Paramétricas da Cônicas
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Classifique as seguintes cônicas degeneradas:
Passo 1
Nesse exercício temos que classificar as cônicas degeneradas que nos são dadas. Lembrando que as cônicas degeneradas são todas aquelas que falamos na teoria, ou seja: origem, retas, circunferência, entre outras. Basicamente, qualquer cônica que não seja elipse, hipérbole ou parábola.
Passo 2
a)
A solução da equação acima é:
Essa solução nada mais é que um conjunto de retas, ou seja, as retas:
O exercício não pede, mas esboçando:
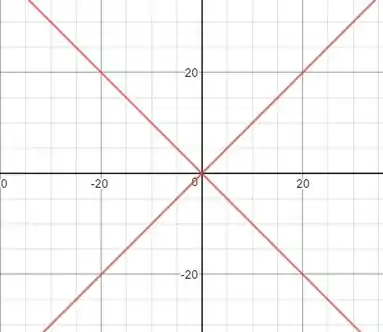
Passo 3
b)
Nesse item temos tanto quanto elevados ao quadrado e a soma deles dando zero. A única solução possível é que e sejam zero, logo:
Então, nossa solução representa a origem do sistema cartesiano.
Passo 4
c)
Agora, para que nossa equação seja válida temos que ter:
Porém, esse resultado é impossível nos reais já que temos a soma de quadrados, e sabe-se que qualquer número real ao quadrado é positivo, então temos a soma de dois números positivos tendo que dar . Pela inviabilidade de solução, temos que a expressão representa o VAZIO.
Passo 5
d)
E agora, como fazemos??
Bem, vamos tentar ajeitar a expressão completando quadrados para que então possamos concluir algo. Completando quadrados teremos:
Nossa equação representa a reta
Passo 6
d)
Ufa!! É a última!!

Para achar qual cônica é, vamos novamente completar quadrados. Teremos:
Olha, é uma circunferência!! Com centro em e raio
Caso você tenha curiosidade de como é a circunferência fizemos um esboço.
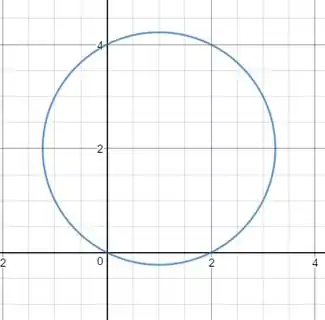
Resposta
Exercício Resolvido #2
Elaboração Própria
Escreva as equações paramétricas das curvas a seguir:
a)
b)
Passo 1
Vamos começar a esquentar nossos motores!! Começar a aplicar tudo o que vimos na teoria!!
E nosso objetivo nesse exercício é escrever as equações paramétricas das cruvas. Bora começar!!

Passo 2
a)
Nossa primeira curva é uma circunferência. Vimos na teoria que para a equação genérica :
Temos as seguintes equações paramétricas:
Então, só substituir:
Pronto!! Já encontramos e em função de e respectivamente.
Passo 3
b)
Agora, temos uma elipse. Também vimos que para uma elipse do seguinte formato:
Temos as equações:
Ué, mas as equações que vimos na teoria não eram assim!! Será que o b e o a não estão trocados??
Já vou responder logo: não estão!!
Aquela fórmula que vimos na teoria serve pra uma elipse com a equação do tipo
Nesse exercício, o b tá em baixo do x, e o a tá em baixo do y.
Quem vai entrar multiplicando o cosseno é cara que tá em baixo do x, ou seja, nesse caso é o b!
E o seno?? Aí vai ser quem tiver em baixo do y (no caso do exercício é o a), beleza??

Show, agora que vimos isso, comparando a equação da elipse que a gente tem com a que eu mostrei pra vocês no início, vemos temos que:
Então, nossas equações paramétricas são:
Essa foi só para aquecer!! Hehe.. Vamos para a próxima!!
Resposta
Exercício Resolvido #3
Elaboração Própria
Determinar a equação retangular da curva cujas equações paramétricas são:
Passo 1
O enunciado pede a equação retangular, mas o que é isso??

Calma!! Você sabe o que é, mas, talvez, nunca tenha ouvido essa expressão!! A equação retangular, é a expressão da curva em função de e , ou seja, escrita no sistema cartesiano ou também chamado de sistema retangular.
Passo 2
Bom, para chegarmos numa relação retangular temos que sumir com os termos e . Para isso, precisamos conhecer uma relação entre esses termos. Da geometria lá do colégio sabemos que:
Se dividirmos essa expressão por , teremos:
Então, vamos tentar manipular a expressão que nos foi dada pelo enunciado para tentarmos usar essa expressão e eliminar os termos que são dependentes da secante e da tangente.
Passo 3
Vamos começar reescrevendo as equações que nos foram dadas de uma forma diferente:
Usando a relação:
Se elevarmos as equações ao quadrado teremos:
Bom, temos o quadrado da tangente e o quadrado da secante. Temos pela expressão que a subtração da secante pela tangente dá um, então é o que faremos:
Pronto, chegamos numa expressão retangular da curva. E por sinal, qual é essa curva?
Como já vimos, é uma hipérbole transladada ;)
Resposta
Exercício Resolvido #4
Elaboração Própria
Seja a curva com equações paramétricas:
Determine .
Passo 1
Bom, quando aprendemos cônicas, vimos todas definidas no sistema cartesiano, ou seja, com e . Então, para conseguirmos identificar a curva com maior facilidade nossa tarefa será sumir com o parâmetro e encontrar uma relação entre e .
Bora começar??
Passo 2
Esse tipo de exercício é meio que tentativa e erro. Então, tem alguns que precisamos ver pelo menos uma vez na vida para ter a sacada. Essse é um deles haha.
Para começar vamos reescrever as expressões dadas:
Se elevarmos ao quadrado teremos:
Passo 3
Vamos, agora, analisar os numeradores das expressões e . Se pegarmos a expressão e subtrairmos da expressão , teremos:
Agora aqui no numerador do último cara da direita temos um quadrado perfeito!
Finalmente,
Logo, temos que:
E essa é a expressão de uma hipérbole!!
Resposta
Exercício Resolvido #5
Elaboração Própria
Determinar os autovalores e os autovetores associados se:
Passo 1
Vamos fazer um aquecimento!! Hehe... para então podermos ir sem nenhuma dúvida para os casos das cônicas com rotação!!
Passo 2
A matriz que nos é dada:
Foi nos dada a matriz e devemos calcular seus autovalores e autovetores. Primeiro, começamos com os autovalores, para isso faremos:
Então,
Calculando o determinante, temos:
Os autovalores são:
Agora, que temos os autovalores podemos calcular o autovetor para cada um dos autovalores. Vamos começar por
Para :
Encontrar o autovetor significa respeitar:
Sendo a matriz dada, , a matriz identidade e o autovetor que queremos descobrir.
Montando a expressão acima e supondo que , teremos:
Como a primeira linha é toda nula, não faz sentido utilizá-la, pois chegaremos que . Então, vamos usar a segunda linha:
Agora, podemos colocar os valores que quisermos desde que respeite a relação. Então, vou dizer que , então será . Pronto temos nosso primeiro autovetor.
Mas, lembre: Nosso autovetor deve ser unitário, ou seja, dividir cada coordenada pela sua norma.
Autovetor unitário será:
Acabamos!! Nada disso!! Falta calcular o autovetor para .
Para , considerando agora que nosso autovetor seja
Escolhendo a primeira ou a segunda linha teremos a mesma relação:
Como não temos nenhuma relação para isso significa que é livre, ou seja, pode ter qualquer valor. Assim, vamos escolher . Portanto:
Como o módulo de é , então ele é nosso próprio autovetor unitário.
Ufa!! Agora sim terminamos!! Hehe
Resposta
Exercício Resolvido #6
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 273-1.
Esboçar o gráfico da cônica de equação
Passo 1
O problema pede para esboçarmos o gráfico da cônica com expressão dada acima. Porém, como podemos notar a expressão possui o termo , o que indica que a cônica está rotacionada. Logo, teremos que desenvolver o método mostrado na teoria para descobrirmos qual é essa cônica e como ela está posicionada.
Passo 2
Como vimos na teoria, devemos começar montando a equação matricial da equação dada. Para isso, vamos primeiro retirar os valores das contantes e .
Da equação temos:
Vamos então colcoar esses valores na equação matricial:
Nossa equação ficará:
Agora que temos nossa equação matricial conseguimos achar nossa matriz , que é:
Próximo passo é calcular os autovalores e autovetores dessa matriz!!
Passo 3
Bora calcular os autovalores da matriz .
Sempre usando a relação
Resolvendo o determinante:
Resolvendo a equação de segunda grau temos:
Passo 4
Já temos os autovalores!! Agora, é encontrarmos os autovetores para cada autovalor.
Para , vamos supor que o autovetor é e devemos respeitar que:
Escolhendo uma das linhas, escolherei a primeira, mas sem um motivo especial:
Poderíamos ter escolhido a segunda linha, o resultado final é o mesmo!!
Então, sabendo a relação e chutando , temos . Assim, nosso autovetor é:
Mas, ele não é unitário. Falta dividirmos por sua norma (módulo) que é .
Então untário é:
Agora, vamos calcular o autovetor para
Escolhendo uma das linhas, escolherei a primeira, mas sem um motivo especial:
Poderíamos ter escolhiso a segunda linha, o resultado final é o mesmo!!
Então, sabendo a relação e chutando , temos . Assim, nosso autovetor é:
Mas, ele não é unitário. Falta divifirmos por sua norma que é
Então untário é:
Passo 5
Agora que temos os autovalores e os autovetores podemos montar as matrizes e .
Montando :
Como foi montada de forma que a primeira linha é o autovalor , então a primeira coluna da matriz deve ser o autovetor relacionado ao autovalor , ou seja, .
Já temos tudo o que precisamos para montar nossa expressão matricial final:
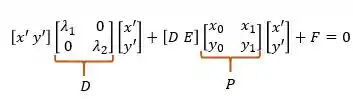
CUIDADO: na expressão acima quando temos [D E], o se refere ao valor que encontramos lá no início do exercício e não a matriz .
Montando com nosso valores teremos:
Fazendo a distributiva, temos:
Vamos completar quadrados:
Dividindo tudo por
Chegamos na expressão de uma elipse. Sendo que a relação entre e é:
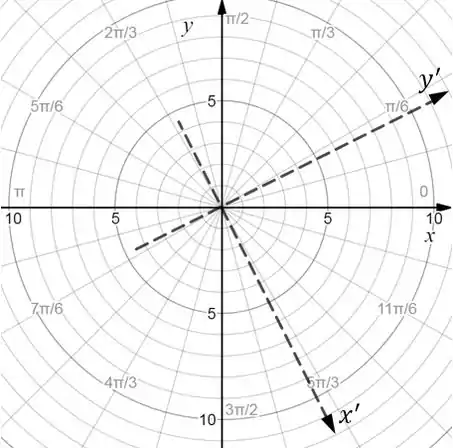
Teremos:
Como queremos um esboço, vamos analisar primeiro a matriz que nos dá o quanto o eixo girou. Como sabemos que:
Temos que:
Então, nosso eixo estará da seguinte forma:
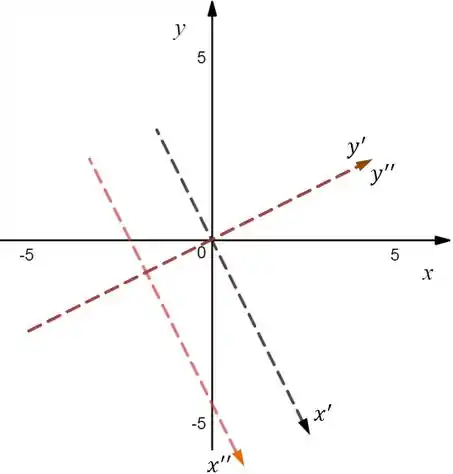
Além disso, nossa elipse possui uma translação em relação ao eixo , tal que:
A gente consegue ver isso pela equação que a gente achou antes, que era:
Basta fazer uma mudança de variáveis, indo de x’y’ para x’’y’’.
Vamos achar o centro de . Para isso, sabemos que o centro de é .
Esboçando teríamos algo do tipo:
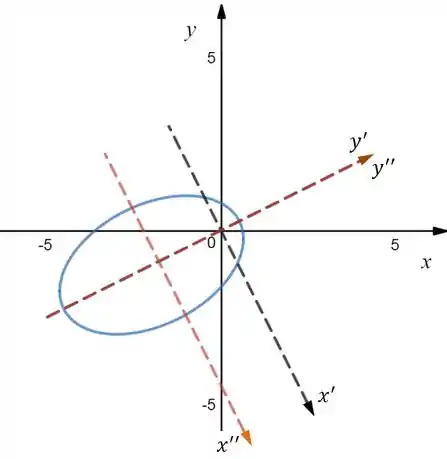
Essa foi mais chatinha!! Mas, deu certo!!

Resposta
Esboço:
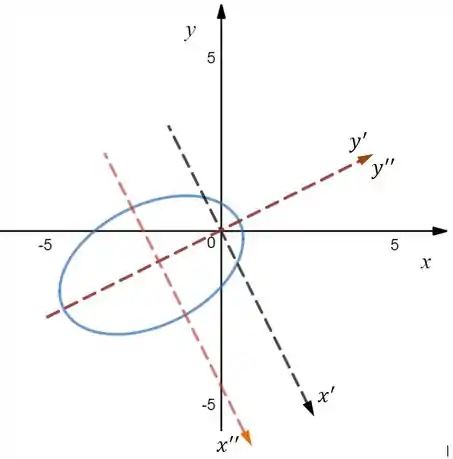
Exercício Resolvido #7
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 275-2.
Esboçar o gráfico da cônica de equação
Passo 1
O mesmo problema do anterior??

Exatamente!! Novamente, vamos esboçar a cônica dada pela expressão acima. Talvez, você ache um pouco chato, mas é fundamental fazermos vários exercícios para fixar bem o passo a passo.
Bora começar então!!
Passo 2
Como vimos na teoria, devemos começar montando a equação matricial da equação dada. Para isso, vamos primeiro retirar os valores das contantes e .
Da equação temos:
Vamos então colocar esses valores na equação matricial:
Nossa equação ficará:
Agora que temos nossa equação matricial conseguimos achar nossa matriz , que é:
Próximo passo é calcular os autovalores e autovetores dessa matriz!!
Passo 3
Bora calcular os autovalores da matriz .
Sempre usando a relação
Resolvendo o determinante:
Temos os valores:
Passo 4
Já temos os autovalores!! Agora, é encontrarmos os autovetores para cada autovalor.
Para , vamos supor que o autovetor é e devemos respeitar que:
Escolhendo uma das linhas, escolherei a primeira, mas sem um motivo especial:
Poderíamos ter escolhiso a segunda linha, o resultado final é o mesmo!!
Então, sabendo a relação e chutando , temos . Assim, nosso autovetor é:
Mas, ele não é unitário. Falta dividirmos por sua norma que é
Então untário é:
Agora, vamos calcular o autovetor para
Escolhendo uma das linhas, escolherei a primeira, mas sem um motivo especial:
Então, sabendo a relação e chutando , temos . Assim, nosso autovetor é:
Mas, ele não é unitário. Falta divifirmos por sua norma que é
Então untário é:
Passo 5
Agora que temos os autovalores e os autovetores podemos montar as matrizes e .
Montando :
Como foi montada de forma que a primeira linha é o autovalor , então a primeira coluna da matriz deve ser o autovetor relacionado ao autovalor , ou seja, .
Já temos tudo o que precisamos para montar nossa expressão matricial final:
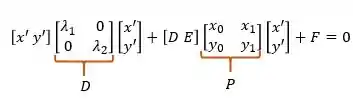
CUIDADO: na expressão acima quando temos [D E], o se refere ao valor que encontramos lá no início do exercício e não a matriz .
Montando com nossos valores teremos:
Fazendo a distributiva, temos:
Rearranjando para ficar na forma um pouco mais parecida com a forma canônica da parábola:
Chegamos na expressão de uma parábola. Sendo que a relação entre e é:
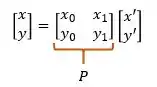
Teremos:
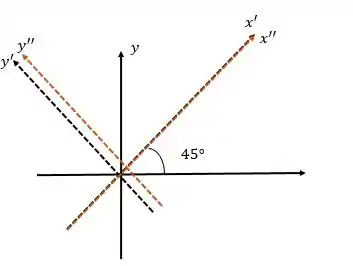
Como queremos um esboço, vamos analisar primeiro a matriz que nos dá o quanto o eixo girou. Como sabemos que:
Temos que:
Então, nosso eixo estará da seguinte forma:
Além disso, nossa parábola possui uma translação em relação ao eixo , tal que:
Vamos achar o centro de . Para isso, sabemos que o centro de é
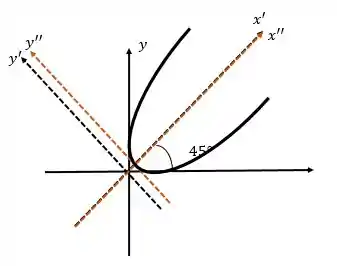
Para esboçar temos que lembrar da teoria do tópico 1 que vimos dois casos principais para a parábola, quando ela estava no eixo ou no eixo . A expressão que obtemos da parábola indica que estamos no CASO 2 da nossa teoria de parábolas.
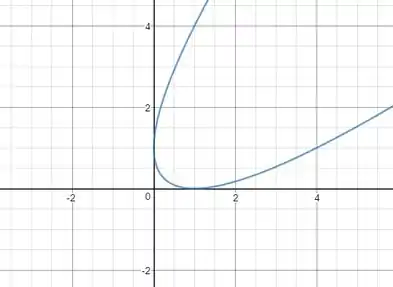
Realmente, plotando com um software, obtemos:
As contas nessa foram mais tranquilas!! Hehe

Resposta
Exercício Resolvido #8
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 277-3.
Esboçar o gráfico da cônica de equação
Passo 1
Poxa!! Não aguento mais!! É eu sei ;)...mais um pouquinho!! Depois desses exercícios você vai tirar de letra cônicas rotacionadas!! Hehe

Então, vamos fazer o mesmo passo a passo até você decorar cada um deles direitinho!! ;)
Passo 2
Devemos começar montando a equação matricial da equação dada. Para isso, vamos primeiro retirar os valores das contantes e .
Da equação temos:
Vamos então colcoar esses valores na equação matricial:
Nossa equação ficará:
Agora que temos nossa equação matricial conseguimos achar nossa matriz , que é:
Próximo passo é calcular os autovalores e autovetores dessa matriz!!
Passo 3
Bora calcular os autovalores da matriz .
Sempre usando a relação
Resolvendo o determinante:
Temos que:
Passo 4
Já temos os autovalores!! Agora, é encontrarmos os autovetores para cada autovalor. Ah sério?! De novo?! Aham!! Força aí!!
Para , vamos supor que o autovetor é e devemos respeitar que:
Escolhendo uma das linhas, escolherei a primeira, mas sem um motivo especial:
Poderíamos ter escolhido a segunda linha, o resultado final é o mesmo!!
Então, sabendo a relação e chutando , temos . Assim, nosso autovetor é:
Mas, ele não é unitário. Falta dividirmos por sua norma que é
Então untário é:
Agora, vamos calcular o autovetor para
Escolhendo uma das linhas, escolherei a primeira, mas sem um motivo especial:
Poderíamos ter escolhido a segunda linha, o resultado final é o mesmo!!
Então, sabendo a relação e chutando , temos . Assim, nosso autovetor é:
Mas, ele não é unitário. Falta divifirmos por sua norma que é
Então untário é:
Passo 5
Agora que temos os autovalores e os autovetores podemos montar as matrizes e .
Montando :
Como foi montada de forma que a primeira linha é o autovalor , então a primeira coluna da matriz deve ser o autovetor relacionado ao autovalor , ou seja, .
Já temos tudo o que precisamos para montar nossa expressão matricial final:
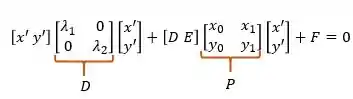
CUIDADO: na expressão acima quando temos [D E], o se refere ao valor que encontramos lá no início do exercício e não a matriz .
Montando com nosso valores teremos:
Fazendo a distributiva, temos:
Vamos completar quadrados:
Chegamos na expressão de um par de retas. Sendo que a relação entre e é:
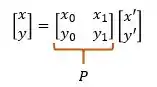
Teremos:
Como queremos um esboço, vamos analisar primeiro a matriz que nos dá o quanto o eixo girou. Como sabemos que:
Temos que:
Então, nosso eixo estará da seguinte forma:
Além disso, nossas retas possuem uma translação em relação ao eixo , tal que:
Antes de continuarmos para ficar claro, nossas retas serão:
Continuando vamos achar o centro de . Para isso, sabemos que o centro de é
Esboçando teríamos algo do tipo:
Realmente, plotando com um software, obtemos:
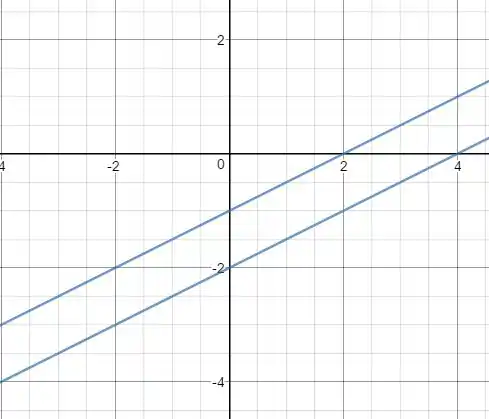
Ufa!! Mais uma se foi!!
Resposta
Exercício Resolvido #9
Unicamp, P3 – Geometria Analítica, 21/06/2013 (manhã), pág. 1, Questão 1
Seja o lugar geométrica dos pontos do plano cujas coordenadas e satisfazem
- Identificar a cônica
- Encontrar as mudanças consecutivas das coordenadas que levam à forma canônica
- Encontrar a excentricidade de . Encontrar também as coordenadas dos focos e dos vértices, e as equações das assíntotas no sistema (se aplicável). Fazer um esboço do gráfico de .
Passo 1
Até agora estávamos esboçando as cônicas!! Nisso já estamos craques!! Hehe... Mas, vamos começar a complicar um pouco mais. Além de fazer tudo o que já fazíamos vamos começar a encontrar não só as cônicas, mas também seus parâmetros.
Passo 2
a) Nesse primeiro item devemos identificar a cônica, ou seja, fazer o que já vínhamos fazendo!
Como vimos na teoria, devemos começar montando a equação matricial da equação dada. Para isso, vamos primeiro retirar os valores das contantes e .
Da equação temos:
Vamos então colocar esses valores na equação matricial:
Nossa equação ficará:
Agora que temos nossa equação matricial conseguimos achar nossa matriz , que é:
Próximo passo é calcular os autovalores e autovetores dessa matriz!!
Bora calcular os autovalores da matriz .
Sempre usando a relação
Resolvendo o determinante:
Temos os autovalores:
Já temos os autovalores!! Agora, é encontrarmos os autovetores para cada autovalor.
Para , vamos supor que o autovetor é e devemos respeitar que:
Escolhendo uma das linhas, escolherei a primeira, mas sem um motivo especial:
Poderíamos ter escolhido a segunda linha, o resultado final é o mesmo!!
Então, sabendo a relação e chutando , temos . Assim, nosso autovetor é:
Mas, ele não é unitário. Falta dividirmos por sua norma que é .
Então untário é:
Agora, vamos calcular o autovetor para
Escolhendo uma das linhas, escolherei a primeira, mas sem um motivo especial:
Então, sabendo a relação e chutando , temos . Assim, nosso autovetor é:
Mas, ele não é unitário. Falta dividirmos por sua norma que é
Então untário é:
Agora que temos os autovalores e os autovetores podemos montar as matrizes e .
Montando :
Como foi montada de forma que a primeira linha é o autovalor , então a primeira coluna da matriz deve ser o autovetor relacionado ao autovalor , ou seja, .
Já temos tudo o que precisamos para montar nossa expressão matricial final:
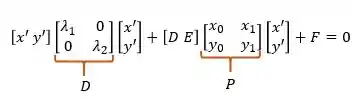
CUIDADO: na expressão acima quando temos [D E], o se refere ao valor que encontramos lá no início do exercício e não a matriz .
Montando com nossos valores teremos:
Fazendo a distributiva, temos:
Completando quadrados:
Dividindo tudo por :
Multiplicando tudo por
Chegamos na forma quase canônica da hipérbole. Para ficarmos na forma canônica faremos mais uma mudança de variável, considerando:
Teremos então:
Agora sim temos a expressão canônica da hipérbole. Esse item terminamos.
Passo 3
b) Agora precisamos determinar as mudanças consecutivas de coordenadas que fizemos para chegar na expressão canônica da hipérbole.
Bom, primeiro, mudamos das coordenadas para . A relação entre esses dois sistemas é dado por:
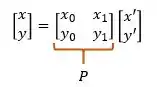
Então, substituindo nossa matriz , temos:
Teremos, então as relações:
Além dessa transformação fizemos uma translação do sistema para . No qual temos as relações:
Pronto!! São essas relações que o enunciado pede. Bora para o próximo item!!
Passo 4
c) Encontrar a excentricidade de . Encontrar também as coordenadas dos focos e dos vértices, e as equações das assíntotas no sistema (se aplicável). Fazer um esboço do gráfico de .
Esse item já fizemos várias vezes quando falamos de cônicas!! O que muda agora, é que antes tínhamos no máximo uma translação, ou seja, uma mudança de variáveis, e agora, temos duas mudanças. Mas, isso não altera a forma de resolução. Ou seja, vamos achar todas as variáveis no sistema em que a curva está no sistema canônico e depois por meio das relações que achamos no item anterior passamos para o sistema .
Então, considerando a equação:
Estamos no CASO 1 da hipérbole. Assim, sabemos que:
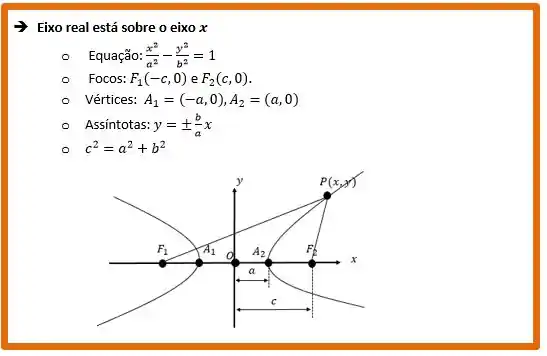
Olhando para nossa expressão e as relações acima, temos:
Usando a relação
Lebrando que todos os parâmetros que encontraremos estarão no sistema .
Teremos:
Encontramos tudo o que percisávamos no sistema , agora vamos passar para o sistema e depois para o sistema . Para a primeira mudança, usaremos:
Usando as relações acima obteremos os parâmetros em :
A excentricidade não muda, pois só depende de e .
Para chegarmos na nossa solução vamos passar do para , usando:
Fazendo as contas, teremos:
Para passar as assíntotas para teremos que primeiro isolar nas nossas relações acima e . Isolando teremos:
Substituindo:
Estamos quase terminando, falta o esboço, que fica mais ou menos:
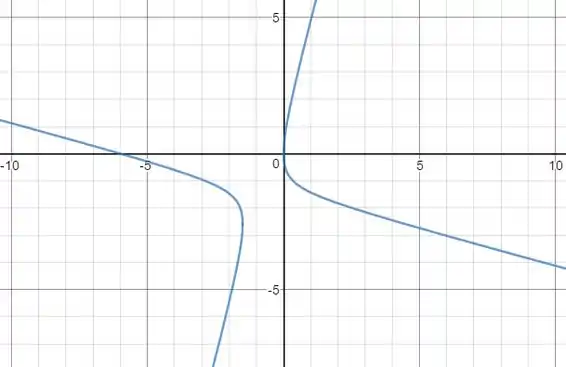
Ufa!! Cansei!! Esse tipo de exercício requer muita atenção por causa das contas que são muito fáceis de errar. Então, faça com calma e para pegar agilidade nada como fazer vários exercícios!
