Superfície Esférica
Produzido por Aline BuzziTeoria
Introdução
Todo mundo já jogou algum esporte seja vôlei, futebol, basquete, ou até outros! Então, você deve reconhecer a figura a seguir hehe

Sabemos o que é uma esfera na prática, mas a pergunta é:
Como definimos uma esfera na geometria analítica?

Relaxa Aí!! Vamos te ensinar tudo o que precisas saber sobre superfícies esféricas!!

Bora começar!!!
Superfície Esférica
No espaço, podemos ter lugares geométricos em formato esférico, tipo assim:
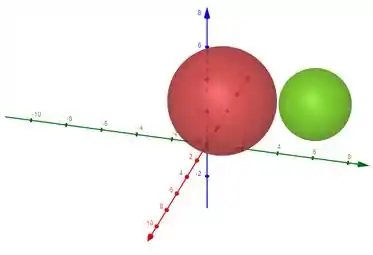
Essas esferas possuem equações próprias para defini-las assim como os lugares geométricos que já vimos beleza? O que precisamos para escrever a equação de uma esfera?
Para definir uma esfera precisamos conhecer as coordenadas do centro da esfera e também o raio da esfera . Assim, definido o centro e o raio, um ponto pertencerá à esfera se satisfizer a seguinte equação:
A equação acima é chamada de equação reduzida da superfície esférica. Guarde com carinho essa expressão que ela será bastante usada!! ;)
Então deixa eu ver, se o centro de uma esfera for e o raio dela for de tamanho 3, qual a equação dela? Essa aqui ó:
E o esboço dessa esfera fica assim:
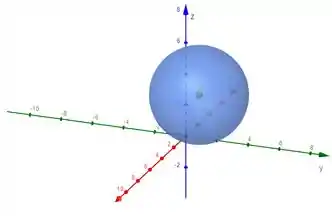
Mas calma!! E se eu tiver uma equação tipo assim:
Que ao invés do centro ser subtraído ele é somado?? O que isso quer dizer?? :O
Caaalma, se o sinal dentro dos parênteses estiver positivo, só significa que aquela coordenada do centro é negativa tendeu? Então nesse caso, o centro seria sacou? E o raio dela é .
Mas e aí, só tem essa forma de escrever a equação de uma superfície esférica? Nada disso!! Outra forma de se escrever é desenvolver os quadrados da expressão acima (por produtos notáveis), e assim obteremos a expressão chamada de equação geral de uma superfície esférica:
Então no exemplo da esfera ali em cima, a equação geral dela é:
Se abrirmos os quadrados da fórmula possuímos:
Já sabemos caracterizar uma superfície esférica com as duas expressões a seguir:

Sendo as coordenadas do centro da esfera, o raio da esfera e e constantes.
Se o exercício der a equação geral e pedir para encontrar a reduzida, basta completar os quadrados novamente ;)
Beleza, já sei caracterizar uma esfera, mas e se eu quiser saber se um ponto pertence à esfera? Ou, se uma reta passa pela esfera?
Vamos ver isso agora!!

Posição relativa de Ponto e Superfície Esférica
Por exemplo, se tivermos aquela esfera do item anterior
E quisermos saber qual a posição relativa dessa esfera com o ponto , como fazemos?
Um ponto tem duas posições relativas:
- Interior à Esfera: Isso ocorre se a distância entre o ponto e o centro da esfera for menor que o raio .
- Exterior à Esfera: Já se o contrário ocorrer, ou seja, o ponto não pertence à esfera.
- Se , então significa que a reta não passa pela superfície esférica, logo, não temos interseção . Na figura a seguir é a imagem a).
- Se , então a interseção entre a reta e a esfera é um único ponto. Sendo que esse ponto é a projeção ortogonal de sobre como mostra imagem b) na figura a seguir.
- Se então a interseção entre a reta e a esfera é formado por dois pontos distintos, e , sendo que o ponto médio entre esses dois pontos representa a projeção do ponto sobre a reta . Imagem c) a seguir.
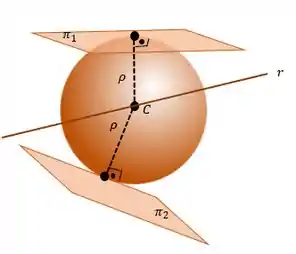
- Se significa que o plano e a esfera não se tocam, logo, a interseção entre eles é nula (Figura A)
- Se então o plano e a esfera se encontram num único ponto, sendo esse a projeção do centro da esfera no plano (Figura B).
- Se , então a interseção, agora, será uma circunferência de raio , contida em , cujo o centro da circunferência é a projeção ortogonal de sobre (Figura C).
- é uma circunferência. Então, dizemos que e são SECANTES.
- . e são DISJUNTAS.
- é um único ponto . e são TANGENTES.
- e são SECANTES se
- e são TANGENTES se
- e são DISJUNTAS se
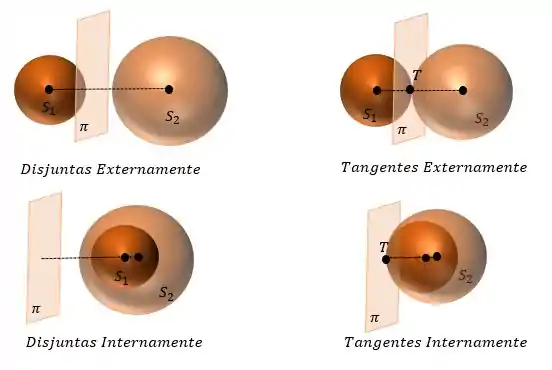
- TANGENTE INTERIORMENTE – se todo ponto de uma das superfícies, diferente de , é interior à outra.
- TANGENTE EXTERIORMENTE – se todo ponto de uma das superfícies, diferente de , é exterior à outra.
- DISJUNTA INTERIORMENTE – Uma das esferas é interior à outra
- DISJUNTA EXTERIORMENTE – Cada uma das superfícies é exterior à outra.
Nesses casos sempre vamos calcular a distância entre o ponto e o centro da esfera. No nosso caso, , então, pela fórmula da distância entre pontos:
Agora vamos ver, sabendo que nosso raio é , temos que . Loogo, o ponto é interior à esfera :D
Interseção e Posição Relativa de Reta e Superfície Esférica
Agora bora falar de reta relacionada à superfície esférica.
Por exemplo, ainda falando da esfera de equação .
Se tivermos a reta
Se calcularmos a distância dessa reta até o centro da esfera obteremos uma distância menor que o raio! O que isso significa?
Significa que essa reta vai ser secante à esfera porque a distância dela até o centro vai ser menor que o raio ;)
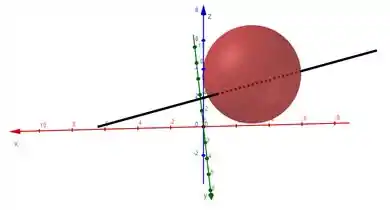
Quando analisamos posição relativa e interseções vemos que as duas estão conectadas. Mas, como?
Bem, vamos analisar os casos a seguir, supondo uma reta e uma superfície esférica de centro e raio :
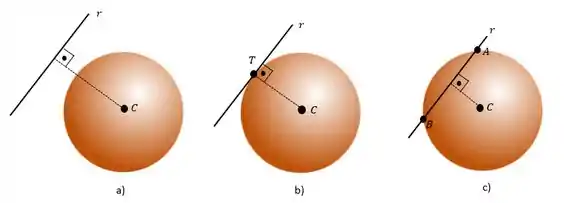
Nos caso da figura b) a reta ela é chamada como reta tangente a superfície esférica. Sendo o ponto de tangência, ou seja, o único ponto em que a reta e a superfície se tocam.
Já na figura c) a reta é chamada de secante, pois possui dois pontos distintos de interseção com a esfera.
Vimos as posições relativas e as interseções! É bom salientar que como vocês podem notar para fazer essas análises precisamos calcular a distância entre ponto e reta. Então, se você não lembra direito como calcular essas distâncias dê uma olhada na teoria de Distâncias no Assunto “ Retas e Planos” ;)
E para planos como ficam essas relações? Próximo tópico ;).
Interseção e Posição Relativa de Plano e Superfície Esférica
A ideia para plano é a mesma que usamos para reta, ou seja, vamos comparar o raio com a distância do plano ao centro da esfera. Assim, considerando o plano e uma superfície esférica com centro e raio teremos os seguintes casos:
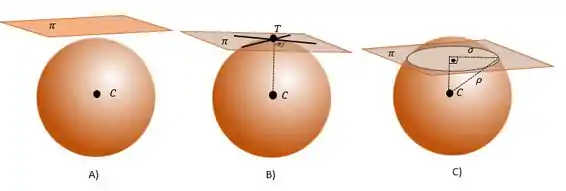
Na figura B) o ponto é chamado de ponto de tangência entre a esfera e o plano . E nesse caso pode ser chamado como plano tangente à esfera. Na figura C) o plano é chamado de plano secante.
Mais uma vez, não custa lembrar, que agora estamos trabalhando com distância entre ponto e plano, então se você não se lembra como calcular essa distância vale a pena voltar na teoria de “Distâncias”!!

Ufa!! Está quase acabando!! Para finalizar nosso estudo sobre superfícies esféricas só falta vermos a posição relativa e interseção entre esferas!! Haha
Interseção e Posição Relativa de Superfícies Esféricas
Vamos supor duas esferas distintas com e e a outra com e . Temos três possibilidades para a posição relativa:
Para facilitar acharmos as interseções suporemos um plano que será perpendicular ao vetor formado pelos centros das esferas . Na figura a seguir temos as possibilidades: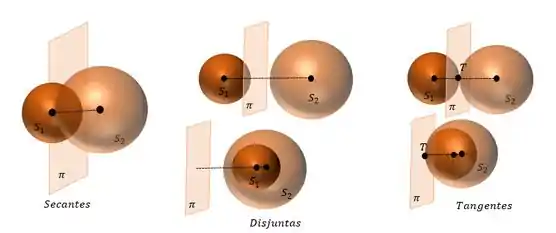
Assim, para obter a interseção ,podemos trabalhar com uma das superfícies e o plano , ignorando a outra. Se escolhermos trabalhar com , temos:
Mas, como encontro o plano ? Realmente, nem sempre encontrar esse plano é uma tarefa fácil. Para isso, temos uma fórmula para facilitar nossa vida hehe. Considerando :

Para terminar vamos ver que duas superfícies disjuntas ou tangentes possuem duas possibilidades como mostra a figura acima, ou seja:
TANGENTE
DISJUNTA
Pronto!! A teoria terminou!!
Bora destruir nos exercícios?!

Superfície Esférica
Posição relativa de Ponto e Superfície Esférica
Interseção e Posição Relativa de Reta e Superfície Esférica
Interseção e Posição Relativa de Plano e Superfície Esférica
Interseção e Posição Relativa de Superfícies Esféricas
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Determinar a equação reduzida e a equação geral da superfície esférica que tenha e raio .
Passo 1
O enunciado pede a equação da superfície que tenha e raio . E devemos encontrar a equação geral e a reduzida.
Passo 2
Pela teoria sabemos que a equação reduzida é da seguinte forma:
Sendo as coordenadas do centro da esfera, o raio da esfera.
Então, se temos que e raio :
Passo 3
A equação geral é da seguinte forma:
Que na verdade nada mais é que a equação reduzida desenvolvida, então desenvolvendo a equação reduzida que encontramos temos:
Já deu para pegar o jeito um pouco?! Mas, ainda temos mais exercícios hehe.. não deixe de fazê-los ;)
Resposta
Exercício Resolvido #2
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 295-2.
Verifique se a equação é a equação de uma superfície esférica. Caso seja, dê o centro e o raio.
Passo 1
Já estamos aquecendo os motores!! O enunciado nos fornece uma equação e pede para verificarmos se ela é ou não a equação de uma superfície esférica. Para isso, vamos completar quadrado e ver se chegamos numa expressão coerente.
Bora começar!!

Passo 2
Vamos começar completando os quadrados:
Pronto chegamos numa expressão com o mesmo jeito da equação da teoria:
Passo 3
Agora que temos a equação, podemos retirar dela as coordenadas do centro e o raio. Assim, da expressão:
Temos que:
Prontinho!! Terminamos!! Uhuuu
Resposta
Exercício Resolvido #3
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 298-7.
Localize os pontos e em relação à superfície esférica
Passo 1
Temos agora a equação de uma superfície esférica e queremos saber a posição relativa dos pontos e , ou seja, se os pontos são internos ou externos à esfera. Como vimos na teoria para verificar a posição entre ponto e reta devemos calcular a distância entre o ponto e o centro da esfera e comparar o valor dessa distância com o raio. Então, primeira coisa que teremos que fazer é achar as coordenadas do centro da esfera e seu raio.
Passo 2
Como a equação que nos foi dada está no formato de equação geral vamos completar quadrados para achar a equação reduzida e então verificarmos as coordenadas do centro e o raio.
Completando quadrados temos:
Com a equação acima conseguimos achar o que precisamos, logo:
Passo 3
Agora, o que temos que fazer é calcular a distância entre o ponto e o centro e comparar com o raio.
Para :
Como , então o ponto é externo à superfície .
Para :
Como , então o ponto é interno à superfície .
Para terminar!!
Para :
Como , então o ponto pertence à superfície .
Mais um exercícios se foi!!

Resposta
Exercício Resolvido #4
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 303-3.
Obtenha equações gerais dos planos tangentes à superfície esférica
Que são paralelos ao plano .
Passo 1
O enunciado pede para obtermos as equações gerais dos planos que são:
- Tangentes à superfície esférica
- Paralelos ao plano .
Passo 2
Vamos começar olhando para a segunda informação que nos foi dada!! Como vimos na teoria sobre planos, se dois planos são paralelos significa que seus vetores normais também são paralelos e como foi dada a expressão geral do plano e essa expressão é do formato:
Sendo as coordenadas do vetor normal, então, a equação dos nossos planos que queremos encontrar será:
Passo 3
Falta, agora, determinarmos o valor de . Para isso, vamos usar a informação em relação à superfície esférica. Sabemos que é tangente aos planos que queremos encontrar e da teoria sabemos que para que um plano e uma esfera sejam tangentes devemos ter:
Então, temos que achar as coordenadas do centro e valor do raio para calcularmos a distância d ponto até o plano que queremos determinar. Para achar e vamos completar quadrados:
Portanto,
Passo 4
Sabendo que e que , vamos usar aquela fórmula, lembra, para calcular distância entre ponto e plano, essa aqui oh:
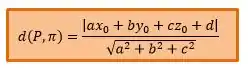
Substituindo os valores, temos:
Como são tangentes:
Então,
Chegamos então nas duas possibilidades de planos tangentes à e paralelos ao plano :
Resposta
Exercício Resolvido #5
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 302-1.
Ache uma equação geral do plano , tangente à superfície esférica pelo ponto .
Passo 1
O enunciado nos fala que o plano que devemos determinar é tangente à superfície e que o ponto de tangência é . Uma forma de terminar um plano é saber o seu vetor normal e um ponto que pertença ao plano. O ponto já temos que é o ponto , o vetor normal podemos achar, pois se encontrarmos o centro da esfera e fizermos o vetor esse será o vetor normal ao plano .
Bora começar!!

Passo 2
Temos que achar primeiro as coordenadas do centro da esfera. Para isso,vamos completar quadrados, mais uma vez!! Hehe
Assim, temos:
Passo 3
Vamos encontrar o vetor :
Como é normal ao plano ,e ntão a equação do plano é:
Para encontrarmos o valor de vamos susbtiutir o ponto :
Então, a equação do nosso plano é:
Resposta
Exercício Resolvido #6
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 310-10.
Ache real tal que as superfícies esféricas e sejam tangentes:
Passo 1
Devemos determinar o valor de para que as superfícies dadas sejam tangentes vamos usar o que aprendemos na teoria. Bora colocar a teoria em prática!! ;)
Passo 2
Da teoria, sabemos que duas superfícies são tangentes, se considerando e :
![]()
Da teoria também conseguimos calcular a distância por meio da fórmula:
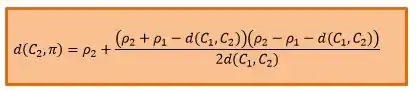
Então, para calcular essa distância precisamos de: . Vamos, então, encontrar esses valores.
Para , temos:
Para teremos que completar quadrado:
Já vamos aproveitar e calcular :
Passo 3
Agora, que temos todos os valores que precisamos podemos calcular a distância :
Susbtituindo na fórmula os valores:
Como queremos que os planos sejam tangentes temos ainda que :
Resolvendo:
Separando em dois casos:
Resolvendo
Resolvendo
Chegamos que para as superfícies e sejam tangentes devemos ter que:
Resposta
Exercício Resolvido #7
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 300-8.
Dê equações na forma simétrica da reta perpendicular ao plano e que contém um diâmetro da superfície esférica .
Passo 1
Queremos determinar as equações simétricas da reta que possui as seguintes características:
- Perpendicular ao plano
- Contém um diâmetro da superfície
Bora começar!!!
Passo 2
Quando estudamos “Retas e Planos” vimos que se uma reta é perpendicular a um plano isso significa que o vetor normal ao plano é paralelo ao vetor diretor da reta, logo, o possível vetor diretor da reta é:
Vetor diretor da reta:
Já sabemos o vetor diretor da reta que queremos determinar. Falta acharmos um ponto que pertença à reta.
Passo 3
Para encontrar o ponto que pertence à reta vamos usar a segunda dica: Contém um diâmetro da superfície. Com essa dica, podemos fazer o seguinte desenho:
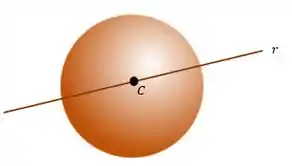
Com o desenho percebe-se que o centro da esfera pertence à reta. Logo, se encontrarmos as coordenadas de temos tudo o que precisamos para definir nossa reta.
Completando quadrado, temos:
Portanto,
Com e :
Simplificando pra ficar bonitinho
Pronto!! Terminamos!!

Resposta
Exercício Resolvido #8
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 306-18.
Calcule para que o plano seja tangente a , e determine o ponto de tangência.
Passo 1
Temos duas informações para encontrar: o valor de para que o plano seja tangente à esfera e determinar o ponto de tangência. Vamos começar determinando o valor de .
Passo 2
Sabemos que para que um plano e uma esfera sejam tangentes, precisamos respeitar a relação:
Para acharmos e que respeita a relação acima, temos, primeiro, que encontrar as coordenadas de e o raio . Para isso, vamos analisar a equação da esfera:
Temos, que:
Para calcular a distância vamos usar a fórmula:
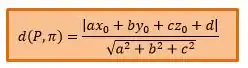
Sendo que da expressão , temos:
Substiutindo temos:
Então,
Vamos fazer o passo a passo para:
Para achar os outros valores é o mesmo esquema ;)
Passo 3
Falta encontrarmos o ponto que é o ponto de tangência. Para achar temos que lembrar da seguinte figura:
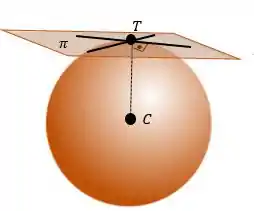
Temos que pertence ao plano , sabemos também que como o plano e a esfera são tangentes, se acharmos duas retas que possuem o ponto essas duas retas serão perpendiculares à reta formada pelo vetor . Se são perpendiculares, podemos usar que:
Então, vamos encontrar dois pontos distintos de e com eles construiremos dois vetores que passam por e que são perpendiculares ao vetor Um ponto para pertencer à deve satisfazer:
Se escolhermos , o valor de . Temos, então nosso primeiro ponto . O segundo ponto pode ser , então . Temos, . Com esses dois pontos podemos construir os vetores:
O vetor é:
Vamos fazer os produtos internos:
Além disso temos que:
Obtemos um sistema:
Substituindo em , temos:
Subsituindo em :
Sendo
Por fim, sabendo que , substuindo em :
Para saber qual é o “correto”, como pertence à deve satisfazer:
Se , então:
Encontramos o ponto .
Ufa!! Terminamos!!

Resposta
Exercício Resolvido #9
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 305-11.
Dê uma equação da superfície esférica tangente aos planos
Cujo centro pertence à reta
Passo 1
Esse exercício é um pouco diferente do que vínhamos fazendo. Queremos novamente determinar a equação da superfície esférica. Mas, agora, as informações que nos são dadas para isso são:
- Superfície tangente aos planos
- Centro da superfície pertence à reta
Teremos que usar essas informações para achar as coordenadas do centro e o raio da esfera. Mas, como faremos isso?

Relaxa!! Vamos fazer o passo a passo!! ;)
Passo 2
Para resolver esse tipo de problema sempre bom fazer um esboço das informações que temos para tentar abstrair e ver como podemos chegar a uma solução!! Então, a figura a seguir seria um bom esboço!
Vamos começar determinando o centro . Sabemos que pertence à reta . Com a relação que nos foi dada, chegamos que:
Então, um ponto genérico da reta possui as seguintes coordenadas:
Então,
Passo 3
Agora, vamos utilizar os planos. Sabemos que os planos são tangentes à esfera. Então, isso significa que a distância entre o plano e é igual a distância entre e , portanto:
Como temos a distância entre um ponto e um plano usaremos a seguinte fórmula:
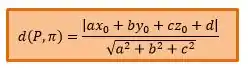
Para o plano :
Para o plano :
Substituindo os valores acima na fórmula e considerando :
Elevando os dois membros ao quadrado e resolvendo:
Temos duas possibilidade para :
Passo 4
Para determinar uma superfície esférica precisamos de e do raio, então vamos calcular uma das distâncias ou , escolhendo e calculando temos:
Para
Para
Portanto, temos como solução duas superfícies esféricas possíveis:
Resposta
Exercício Resolvido #10
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 311-13.
Obtenha as equações gerais das superfícies esféricas com centro que tangenciam interiormente a superfície esférica .
Passo 1
Mais uma vez queremos descobrir as superfícies esféricas que tangenciam interiormente a superfície . Sabemos da teoria que para serem tangentes , mas e para serem tangentes interiormente? Bom, aí você precisa de uma informação que ainda não falamos que é a seguinte:
Supondo que :
- Se, e são tangentes exteriormente
- Se são tangentes interiormente
Sabendo disso conseguimos resolver o exercício!!
Passo 2
Precisamos determinar o valor de para determinarmos as superfícies tangentes à , pois já temos que , então, falta determinarmos: para então aplicarmos a fórmula. Lembrando que estamos assumindo que as superfícicies que queremos encontrar possuem , pois são internas à .
Completando quadrado de :
Portanto:
Passo 3
Usando a fórmula:
E sabendo que para tangenciarem:
Então,
Subsituindo os valores:
Como estamos lidando com distâncias, vamos considerar que:
Assim, temos dois valores possíveis de :
Para verificar se os dois fazem sentido, vamos verificar se
Para :
Para :
Assim, nossas superfícies possíveis são: