Cônicas com Rotação – Método Matricial
Produzido por Aline BuzziTeoria
Introdução
Beleza, vimos como definir parábolas, elipses e hipérboles no plano com elas estando no eixo ou no eixo .
Mass, e se ela não estiver ao longo de nenhum dos dois eixos? Tipo assim:
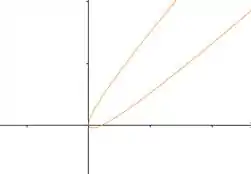
Nessa imagem a gente tem uma parábola meio tortinha não é? Ela está rotacionada.
Agora vem a pergunta: como analisamos cônicas rotacionadas? Quais as suas equações?

Não se assusta não, vamo lá entender isso direitinho :D
Equação Geral das Cônicas
Qualquer cônica, estando ela de qualquer maneira, pode ser escrita pela equação geral:
![]()
Ou seja, se tivermos a equação da elipse: , podemos escrever ela na forma geral assim:
Nesse caso, , , e o restante dos coeficientes é .
O nosso conflito na rotação de cônicas vai ser esse tal desse termo . Sempre que ele aparecer na nossa equação, a cônica vai estar rotacionada :O Ou seja:
- Se , a cônica não vai estar rotacionada, talvez no máximo transladada
- Se , o termo vai existir ali e portanto a cônica vai estar rotacionada
Opa, mas e aí, como fazemos se o for diferente de 0??? É exatamente o que vamos ver agora ;D
Ah, um lembrete: sempre que e/ou for diferente de , a cônica vai estar transladada beleza?
Rotacionando os eixos
Já vimos que quando temos aquele termo na nossa equação, a cônica estará rotacionada certo?
Vamos supor o seguinte, aqui temos uma hipérbole no nosso sistema , o famoso já conhecido:
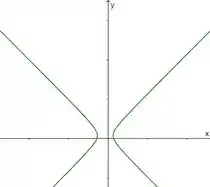
Mas se rotacionarmos essa hipérbole em um ângulo , ela sai desse sistema e passa a estar ao longo do sistema (alguns livros usam , mas no final dá na mesma viu?)
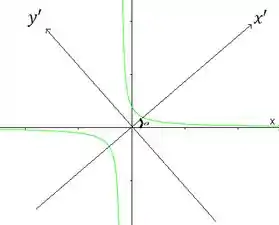
Normalmente, o problema vai dar a equação da cônica rotacionada no sistema e aí pra descobrirmos qual cônica é aquela, transformamos ela no sistema (ou ).
Vamos usar como exemplo a equação geral , que também pode ser escrita assim:
Os coeficientes dessa equação, comparando com a equação geral que demos lá em cima, são:
Nessa equação temos o termo né? Então ela ta rotacionada e precisamos achar sua equação no sistema de coordenadas .
Deixa eu te mostrar um passo a passo de como fazer isso:
Passo 1 – Encontrar o ângulo de rotação
Antes de qualquer coisa, precisamos entender: a que ângulo a cônica “original” foi rotacionada? Será que foi ? Ou ? Hehe pode ter sido qualquer ângulo, e pra descobrir vamos usar a relação:
Então, no nosso exemplo:
Epa!! Como assim uma divisão por 0???
Calma, isso só quer dizer que a tangente do ângulo não existe. Agora vamos pensar, qual é o ângulo que a tangente não existe?? certo? Então:
Então, pra facilitar sua vida: sempre que , o ângulo de rotação vai ser , caso contrário vamos ter que usar a relação mesmo pra resolver :P
Passo 2 – Mudando os eixos
Agora vamos usar uma relação entre o sistema e o , guarda bem isso aqui hein:
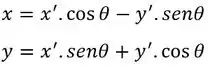
Essa relação vem de que
Por isso chamamos de forma matricial :)
(se seu livro estiver utilizando a notação , é só trocar por e por )
No nosso exemplo, , então:
Passo 3 – Encontrando os novos coeficientes e
Na nossa equação no sistema temos nossos coeficientes e , que no nosso exemplo são e .
Para nossa equação no sistema , vamos encontrar os coeficientes e pelo sistema:
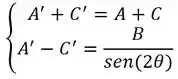
Então, no nosso exemplo:
Resolvendo esse sistema, temos que e
Vamos guardar esses valores e ir pro próximo passo.
Passo 4 – Encontrando a parte linear da equação
Essa parte a gente só vai fazer se a cônica estiver transladada, ou seja, se e/ou for diferente de 0.
Vamos substituir as equações e (aquelas do passo 2) na parte linear da equação original, ou seja, nas partes que multiplicam e :
Então, no lugar de da nossa equação, vamos escrever fechou?
Passo 5 – Escrevendo nossa equação no sistema
Agora sim, finalmente vamos escrever nossa equação no novo sistema de coordenadas, ela vai ficar assim:
Repara que agora nosso termo sumiu, porque no novo sistema de coordenadas, essa cônica não ta rotacionada :D
Pra identificar qual é a cônica, é só completar quadrados em (pois está transladada) e fazer os ajustes necessários. Por fim, vamos descobrir que é uma hipérbole, abaixo temos o esboço dela rotacionada (verde) e depois de fazermos todos esses passos (vermelha)
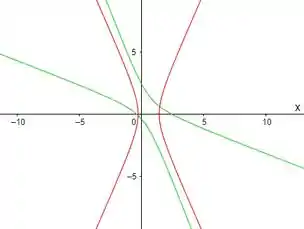
Pra qualquer outra cônica rotacionada, os passos vão ser os mesmos viu?
Agora bora lá fazer exercício pra treinar essa receita de bolo :D
Rotacionando os eixos
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria.
Dadas as equações de cônicas abaixo, determine seus coeficientes na equação geral.
a)
b)
c)
d)
e)
Passo 1
Vimos que a equação geral de uma cônica é dada no formato:
O que precisamos fazer nesse exercício é dar os coeficientes , , ... De acordo com as equações dadas. Vamo lá!!
Passo 2
a) Nossa equação já está na forma geral, agora é só acharmos os coeficientes.
O vai ser o coeficiente que multiplica , logo,
multiplica :
multiplica :
Opa, esses são os únicos coeficientes dessa equação, então podemos dizer que fechou?
Passo 3
b) Agora temos que:
Passo 4
c) Dessa vez:
Passo 5
d) Vamos transformar na equação geral de uma cônica passando o pro outro lado:
Fechou, agora sim podemos falar que:
Passo 6
e) Vamos transformar na equação geral:
Organizando os termos pra facilitar nossa vida:
Daí temos que:
Resposta
a)
b)
c)
d)
e)
Exercício Resolvido #2
Elaboração própria.
Considere as afirmativas a seguir:
I – A cônica não está transladada, mas está rotacionada.
II – O ângulo de rotação da cônica é .
III – A cônica está rotacionada, mas não está transladada.
Estão corretas apenas as afirmativas:
a) I
b) II
c) III
d) I e II
e) I e III
f) II e III
g) I, II e III
Passo 1
Vamos analisar cada uma das afirmativas:
I – Vimos que para uma cônica estar rotacionada, devemos ter o termo , enquanto para estar transladada devemos ter o termo e/ou o termo .
Nesse caso, temos , logo, ela está rotacionada. Mas não temos nem nem , portanto, ela não está transladada. Então a afirmativa é verdadeiraaa :D
II – Bora calcular o ângulo de rotação pela formulazinha que vimos:
Obaaa! Então a afirmativa ta correta!!
III – Abrindo o quadrado de :
Temos o termo e temos o termo , então a cônica está tanto rotacionada quanto transladada. Logo, a afirmativa é falsa :/
Então, a alternativa correta é a letra D! :)
Resposta
d) I e II
Exercício Resolvido #3
IME – UNICAMP, Exercícios de rotação.
Considere o plano com o sistema cartesiano canônico e faça uma rotação de um ângulo obtendo um novo sistema . Seja um ponto do plano.
a) Se no sistema , encontre as coordenadas de no sistema .
b) Transforme a equação para o sistema .
Passo 1
Vimos que a relação entre o sistema e o sistema pode ser dada por
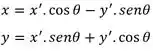
Então, sabendo , vamos utilizer essa relação para resolver os dois itens.
Passo 2
a) Substituindo o ponto , e na relação do passo 1, temos:
Resolvendo esse sistema, encontramos que e .
Então o ponto (ponto no sistema ) é .
Passo 3
b) Temos que
Basta substituirmos essa relações de e em para obtermos essa equação no sistema . Assim:
Resposta
a)
b)
Exercício Resolvido #4
Elaboração própria.
Identifique e esboce a cônica dada pela equação
Passo 1
Temos um na nossa equação, então, a cônica está rotacionada certo?
Pra eliminar o termo misto, vamos fazer uma rotação, mas antes vamos encontrar o ângulo :
Como , o nosso vale .
Pelas relações de mudança de coordenada de para , vamos ter o sistema
Passo 2
Tendo e em função de e , agora a gente vai substituir isso lá na equação do enunciado demorou? (lembrando que como não temos e nem , não precisamos encontrar os coeficientes e )
Agora vamos dividir tudo por 4:
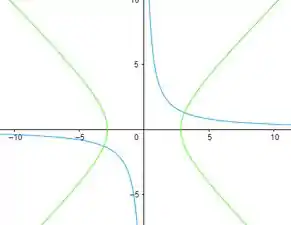
Boa, isso nos dá uma hipérbole com centro . Abaixo temos essa hipérbole esboçada no sistema (verde) e no sistema (azul)
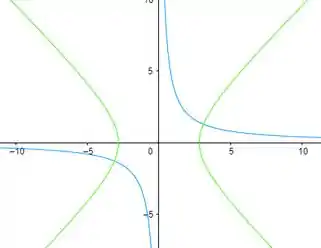
Resposta
Hipérbole.
Exercício Resolvido #5
UFPE, Geometria Analítica, Prova 3, 2015_1, Questão 2
Determine a equação reduzida e identifique a cônica dada pela equação abaixo. Esboce e indique apenas os parâmetros geométricos.
Passo 1
A equação da cônica tem um termo , ou seja, ela está rotacionada fechou? Vamos utilizar o método matricial pra conseguirmos a equação dela no sistema de coordenadas .
Como nos coeficientes da equação da cônica temos que , o nosso ângulo de rotação vai ser certo?
Substituindo naquelas relações da mudança de eixos que vimos, vamos ter:
Passo 2
Vamos agora encontrar os coeficientes e , lembrando que eles vão ser dados pelo sistema
Resolvendo esse sistema, temos que e .
Passo 3
O próximo passo é substituir as relações que encontramos pra e na parte linear da equação original:
Então a parte linear da nossa equação no sistema vai ser
Passo 4
A equação da cônica no sistema , então, vai ser dada por
Dividindo tudo por 2:
Agora vamos ajustar essa equação pra descobrirmos que cônica é essa beleza?
Completando quadrados em :
Passo 5
Fazendo a translação com e , nossa equação fica assim
Dividindo tudo por 4:
Isso nos dá a equação de uma hipérbole certo? :)
Os parâmetros geométricos dela são
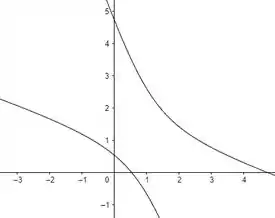
O esboço dela é mostrado abaixo
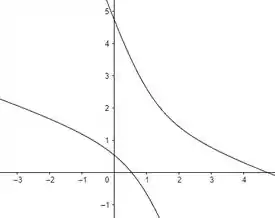
Resposta
Hipérbole.
Exercício Resolvido #6
UFF, Aula de rotação, Katia Frensel
Reduza, por uma rotação dos eixos coordenados, a equação
Determine o foco, o vértice e a diretriz da cônica nas coordenadas , .
Passo 1
Encontrando o ângulo de rotação
Como temos um termo misto , vamos ter que fazer uma rotação certo?
Vamos usar a relação pra descobrir o ângulo:
No nosso caso, , e
Opa, mas como , o nosso ângulo vai ser , lembra??
Boaa, primeiro passo realizado!!
Passo 2
Convertendo o sistema para
Vamos converter o sistema (equação do enunciado) no sistema (cônica rotacionada) usando a relação:
Sabendo que :
Agora precisamos achar os coeficientes e da nossa cônica.
Passo 3
Encontrando os coeficientes e , análogos a e
Os novos coeficientes e vão ser dados pelo sistema:
Na nossa equação original, , então .
Além disso,
Então:
Somando as duas equações, temos
Substituindo na primeira linha:
Ou seja, não teremos o termo na nossa nova equação (pois ), enquanto o termo será multiplicado por .
Passo 4
Encontrando os termos lineares
Agora, vamos substituir as relações do sistema na parte linear da equação do enunciado.
Ou seeeja, vamos substituir no lugar dos termos da equação original :D
Passo 5
Escrevendo a nova equação
Com os coeficientes , e o termo linear, vamos substituir na equação (lembrando que mantemos o termo independente ):
Ajustando a equação:
Ou seja, temos uma parábola :)
Seu vértice no sistema é , seu parâmetro é , e logo, seu foco é .
Passo 6
Usando as equações do sistema pra transformar o foco e vértice pro sistema :
Então no sistema e .
Resposta
e
Exercício Resolvido #7
Lista de exercícios de translação e rotação de cônicas, Prof. Paulo Laerte Natti - Adaptado
Coloque a equação dada abaixo na forma padrão de uma equação de cônica. Para isto realize uma rotação e/ou uma translação de eixos.
Passo 1
Encontrando o ângulo de rotação
Como temos um termo misto , vamos ter que fazer uma rotação beleza?
Descobrindo o ângulo:
Boa, então vamos rotacionar nossa cônica em :)
Passo 2
Convertendo o sistema para
Pela relação de transformação de para :
Sabendo que e :
Agora precisamos achar os coeficientes e da nossa cônica.
Passo 3
Encontrando os coeficientes e , análogos a e
Os novos coeficientes e vão ser dados por:
Somando as duas equações:
Substituindo na primeira linha:
Passo 4
Encontrando os termos lineares
Agora, vamos substituir as relações do sistema na parte linear da equação do enunciado, que no caso é só hehe
Então vamos substituir no lugar de na equação original ok?
Passo 5
Escrevendo a nova equação
Vamos escrever nossa nova equação da seguinte maneira:
Como tudo está dividido por 2, podemos apenas escrever:
Passo 6
Descobrindo a cônica
Completando quadrados:
Dividindo tudo por :
Passo 7
Agora vamos realizar uma translação assim:
Substituindo na nossa equação:
Agora sim, temos nossa equação devidamente rotacionada e transladada :)
Resposta
Exercício Resolvido #8
UFPE – Geometria Analítica – 2015.1 – Prova Final – Questão 3
Determine a equação reduzida e identifique a cônica dada pela equação abaixo. Esboce e indique as coordenadas dos focos no sistema de coordenadas .
Passo 1
Bom, vamo lá, a gente tem uma equação geral de uma cônica. Os coeficientes dela são
Como , essa cônica está rotacionada.
Além disso, como , ela não está transladada, ufaa!
Nesse caso, , então o ângulo não é e podemos demorar um pouco mais pra acharmos a equação reduzida, mas nada impossível viu?
Então bora lá ajustar essa belezinha pro sistema de coordenadas .
Passo 2
Precisamos descobrir pelo menos para descobrirmos os coeficientes e . Sabemos que
Passo 3
Achando a (é só inverter hehe)
Beleza, mas o que queremos é , temos por relação trigonométrica:
Agora que temos o podemos seguir em frente :D
Passo 4
ENCONTRANDO OS COEFICIENTES A’ E C’
Vamos descobrir os coeficientes e :
Somando as duas equações:
Substituindo na segunda equação:
Boaa, achamos os coeficientes e :)
Passo 5
ESCREVENDO A EQUAÇÃO REDUZIDA EM X’OY’
Como a equação não tem parte linear, agora vamos só reescrever a equação no sistema :
Dividindo tudo por :
Isso é a equação de uma elipse ao longo do eixo , onde , e .
Então os focos dessa elipse, no sistema são e .
ENCONTRANDO OS FOCOS NO SISTEMA XOY
Opa, mas queremos os focos no sistema !! E agora??
Para transformar as coordenadas do sistema em , temos a relação
Mas pra acharmos as coordenadas de e no sistema , precisamos de e !!
Passo 6
- Encontrar e
Tendo o sistema:
Podemos desenvolver a segunda equação assim:
Substituindo os valores que temos:
Então, nosso sistema fica assim
Passo 7
Somando as duas equações do sistema:
Substituindo isso na primeira equação:
Boaaa, agora podemos substituir naquela relação pra acharmos as coordenadas dos focos no sistema !!
Passo 8
- Substituindo na relação
Voltando à relação:
Vamos substituir as coordenadas dos focos e :
Então, as coordenadas dos focos no sistema são e .
Abaixo temos essa elipse nos dois sistemas de coordenadas
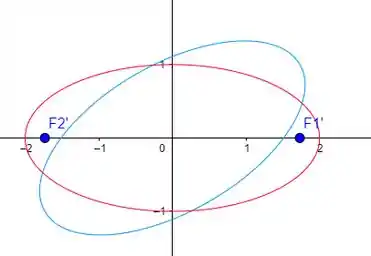
Resposta
e