Quádricas
Teoria
Fala aí, seja bem vindo ao Responde Aí! Bora conhecer as superfícies Quadricas?
Superfícies Quadrícas
Existem váarias superfícies quádricas e a gente vai conhecer as mais importantes hoje, além das duas equações!
As superfícies quádricas são descritas pela seguinte equação geral de
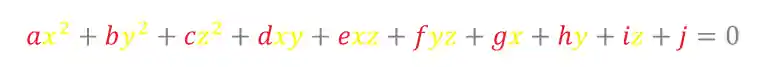
Onde
📢 Clique para saber mais:
Elipsóide
A elipsóide tem essa carinha aqui:
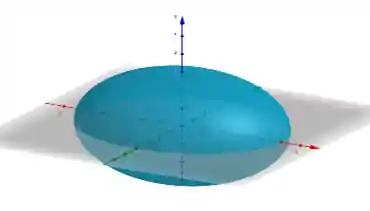
O formato da elipsoide lembra um ovo, ou então o formato da terra que é achatadinho nos extremos! Ela é descrita pela seguinte equação:
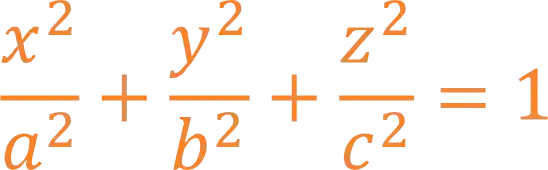
Hiperbolóide De Uma Folha
A hiperbolóide de uma folha tem a equação bem parecida com a da elipsoide, sua única diferença é a presença de um sinal negativo. Saca só:
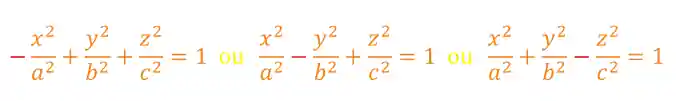
Quando plotamos a hiperbolóide de uma folha, ela fica assim:
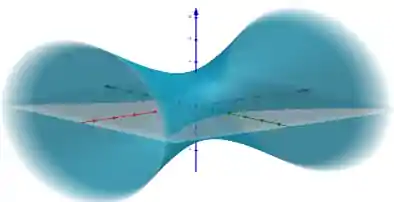
As torres de refrigeração de usinas nucleares tem o formato um hiperbolóide de uma folha. Assim como a Catedral de Brasília!
Hiperbolóide De Duas Folhas
Agora, se pegarmos a equação da hiperbolóide de uma folha e adicionarmos mais um sinal negativo, temos uma hiperbolóide de duas folhas!
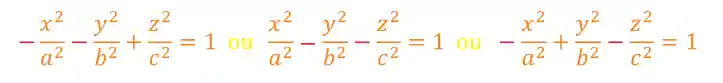
Ela tem essa carinha aqui:
Quer aprender mais sobre quádricas? Conhecer os outros tipos?! Então se liga nesse vídeo aqui 👇
Parabolóide Elíptico
O formato do Parabolóide elíptico se assemelha a uma rede de pesca!
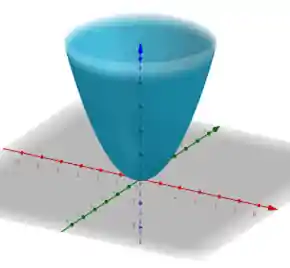
As possíveis equações estão a seguir:
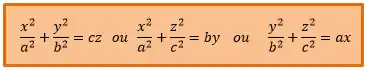
Considerando
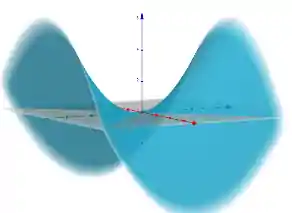
Parabolóide Hiperbólico
A figura do parabolóide hiperbólico se parece uma cela, então muitas vezes essa quádrica é também chamada de cela.
Na sua equação os termos quadráticos possuem sinais contrários:
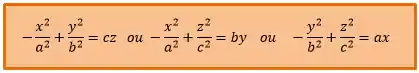
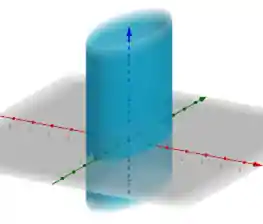
Cilindro Elíptico
O Cilindro Elíptico tem o formato de um cilindro achatado pois, ao invés da base ser circular, ele tem uma base elíptica. Possui uma das seguintes equações reduzidas:
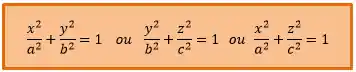
Seu gráfico fica assim:
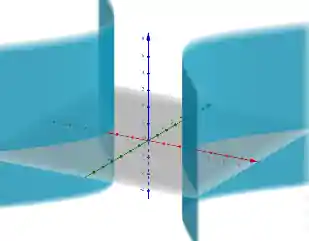
Cilindro Hiperbólico
Tente imaginar uma hipérbole em 3D, provavelmente você pensará num cilindro hiperbólico:
Suas equações reduzidas são:
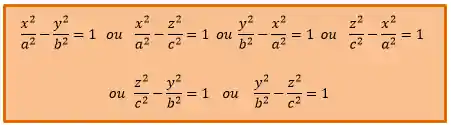
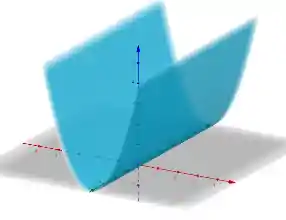
Cilindro Parabólico
O cilindro parabólico é como se fosse uma parábola em 3D, assim:
Suas equações reduzidas podem ser escritas:
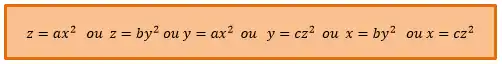
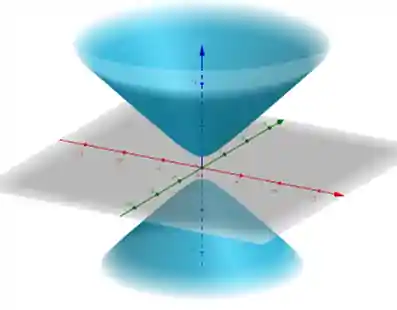
Cone Elíptico
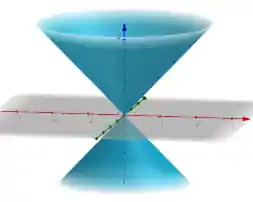
E finalmente chegamos na última quadrática! O cilindro elíptico tem essa carinha aqui:
As equações reduzidas possíveis são:
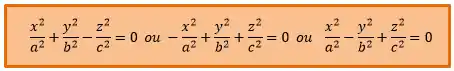
Agora vamos praticar com exercícios?
Parabolóide Elíptico
Parabolóide Hiperbólico
Cilindro Elíptico
Cilindro Hiperbólico
Cilindro Parabólico
Cone Elíptico
Exercícios Resolvidos
Exercício Resolvido #1
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 289-1. Modificado.
Identificar as quádricas representadas pelas equações:
Passo 1
Bora aquecer os motores?? Vamos começar classificando as quádricas!! O que teremos que fazer nesse exercício é manipular as equações que nos foram dadas de forma a chegar na forma canônica que vimos na teoria. Para facilitar a nossa vida, vamos fazer uma lista com as quádricas que vimos:
Elipsóide
Hiperboloide de 1 Folha
Hiperboloide de 2 Folhas
Parabolóide Elíptico
Parabolóide Hiperbólico
Cilindro Elíptico
Cilindro Hiperbólico
Cilindro Parabólico
Já temos todas as possibilidades listadas acima. Então, é só colocar na forma canônica e dar os nomes ;)
Passo 2
a)
Deixando a constante igual a , teremos:
Olhando na nossa lista acima, temos que essa é a equação de um ELIPSÓIDE.
A primeira já fizemos ;)
Passo 3
b)
Novamente, deixando o termo constante igual a , teremos:
Nesse caso temos apenas um termo com sinal negativo. Então, lembrando da nossa dica: UM SINAL NEGATIVO EQUIVALE ao HIPERBOLÓIDE DE UMA FOLHA.
Passo 4
c)
Aplicando o mesmo procedimento do anterior:
Agora, temos DOIS sinais negativos no termo quadrático. Então, temos um HIPERBOLÓIDE DE DUAS FOLHAS.
Passo 5
d)
Note que agora temos um termo que não está elevado ao quadrado, então ficaríamos com a expressão:
Pela nossa lista acima temos um PARABOLÓIDE ELÍPTICO.
Passo 6
Ufa!! Só mais uma heheh
e)
Só deixando os coeficientes dos termos quadráticos iguais a :
Olhando nossa lista, temos um PARABOLÓIDE HIPERBÓLICO
Prontinho!! Terminamos!!
Resposta
Exercício Resolvido #2
UFF, Lista 5 – Geometria Analítica e Cálculo Vetorial, pág 1, ex. 3
Encontrar os pontos de interseção do parabolóide hiperbólico com a reta
Passo 1
Para encontrar os pontos de interseção esses pontos devem satisfazer as duas equações:
Passo 2
Primeiro, para facilitar nossa análise, vamos passar a equação da reta para a forma paramétrica. Teremos:
Essas três expressões devem satisfazer
Substituindo:
Resolvendo:
Passo 3
Tendo os valores de , vamos substituir nas equações paramétricas e descobrir as coordenadas dos pontos.
Para :
Teremos então o ponto .
Para :
Ponto .
Encontramos os pontos que interceptam o paraboloide hiperbólico.
Resposta
Exercício Resolvido #3
UFF, Lista 5 – Geometria Analítica e Cálculo Vetorial, pág 2, ex. 4
Encontre as coordenadas dos focos da elipse que resulta da interseção de com
.
Passo 1
O enunciado já fala que a interseção do parabolóide elíptico com o plano será uma elipse. Então, para achar a elipse resultante basta substituirmos na equação do paraboloide. Ficaremos com:
Deixando na forma canônica, teremos:
Passo 2
Já temos a expressão da elipse, agora, precisamos encontrar as coordenadas dos focos. Lá da teoria de “Cônicas” temos o seguinte resumo:
Como o maior valor do denominador está sobre o , então realmente estamos no caso em que o eixo maior está sobre o eixo do .
Vamos então, primeiro retirar os valores que precisamos. Da expressão:
Temos que:
Usando a relação do resumo acima encontramos o valor de :
E todas essas contas que fizemos valem para ! Então, as coordenadas dos focos da elipse serão:
Acabouuuu!!!
Esse tipo de exercício é importante para percebermos como os assuntos estão conectados e que devemos estar com a teoria afiada ;).