Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Determinantes e Transformações Lineares

Ver Todos os Exercícios

Teoria

Bom, lembra que toda matriz é uma T L ? Então existe alguma ligação entre determinantes e transformações lineares né?

Mas como definimos o determinante de uma transformação linear T : V → V ?

Bom, sabemos achar o determinante de uma matriz, mas uma T L pode ser definida como várias matrizes distintas dependendo da base escolhida para o espaço V . E agora, como faz?

Não tema, pois eu tenho uma ótima notícia pra você! A matriz que representa T em qualquer base de V escolhida terá sempre o mesmo determinante!!

Logo, podemos definir o determinante da transformação T como:

det ⁡ T = det ⁡ A

onde A é a matriz que representa T em uma base qualquer.

Determinante e Mudança de Área/Volume

Imaginem que temos dois vetores formando um paralelogramo no R 2 , ou três vetores formando um paralelepípedo no R 3 . O que aconteceria se aplicássemos uma transformação T nesses vetores?

Parece bom demais pra ser verdade, mas o que aconteceria é que a área ou o volume seriam multiplicados pelo módulo do determinante de T !!

Veja esse exemplo abaixo:

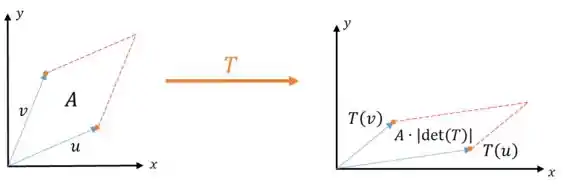
Temos os vetores v e u dados por:

v = 1 , 5 2 ; u = 5 2 , 1

E a transformação T é dada por:

T x , y = 3 x 2 , y 2

Calculando os vetores transformados temos:

T v = 3 2 , 5 4

T u = 15 4 , 1 2

Agora vamos calcular a área pelo método que já estamos acostumados:

A ' = 3 2 15 4 5 4 1 2 = 3 2 ∙ 1 2 - 15 4 ∙ 5 4 = 3 4 - 75 16 = - 63 16

A área então é o módulo do valor que achamos. Agora vamos multiplicar a área A pelo módulo do determinante da transformação:

A = 1 5 2 5 2 1 = 1 - 5 2 ∙ 5 2 = 1 - 25 4 = - 21 4

Uma matriz para T é:

T x , y = 3 x 2 y 2 = 3 2 0 0 1 2 x y ⇒ T = 3 2 0 0 1 2

det ⁡ T = 3 2 0 0 1 2 = 3 4

Finalmente,

A ' = A ∙ det ⁡ T = 21 4 ∙ 3 4 = 63 16

Maneiro né? Isso funciona pra qualquer T L , tanto para áreas quanto para volumes ;)

Obs.: Não sei se você lembra, mas se não lembra pode deixar que eu lembro pra você haha. Quando falamos de matrizes ortogonais, chegamos à conclusão de que seu determinante era sempre igual a 1 ou - 1 . Mas naquela hora não podíamos chegar ao significado por trás disso. Bom, agora podemos!

Lembra dos exemplos que eu dei de matrizes ortogonais? A matriz identidade, a matriz rotação e a matriz reflexão! Repare que nenhuma delas deforma ou altera o tamanho do vetor!! Justamente por isso que seu determinante é sempre igual a ± 1 ! Como elas só giram os vetores ou os mantém inalterados elas não vão alterar a área ou o volume gerado pelos vetores.

Determinante e Mudança de Área/Volume

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

Prove que o determinante de T β ← β é igual ao determinante de T α ← α , qualquer que sejam α e β .

Passo 1

Bom, primeiro passo a fazer é tentar equacionar, já que não tem nenhuma relação que nos ajude sem isso. Lembra da fórmula abaixo?

T β ← β = I d β ← α T α ← α I d α ← β

Agora é só aplicar o determinante dos dois lados:

det ⁡ T β ← β = det ⁡ ( I d β ← α T α ← α I d α ← β )

Passo 2

Lembre-se que det ⁡ A ⋅ B = det ⁡ A ⋅ d e t ⁡ ( B ) . Então aplicando na fórmula acima:

det ⁡ T β ← β = det ⁡ ( I d β ← α T α ← α ) ⋅ det ⁡ I d α ← β ⇒

det ⁡ T β ← β = det ⁡ I d β ← α ⋅ det ⁡ T α ← α ⋅ det ⁡ I d α ← β

Agora é só lembrar que

I d β ← α = I d α ← β - 1 ⇒ det ⁡ I d α ← β - 1 = det ⁡ I d β ← α = 1 det ⁡ I d α ← β

Assim aplicando isso na fórmula:

det ⁡ T β ← β = 1 det ⁡ I d α ← β ⋅ det ⁡ T α ← α ⋅ det ⁡ I d α ← β

Passo 3

-

Agora podemos cancelar os termos!

det ⁡ T β ← β = det ⁡ T α ← α ⋅ 1 det ⁡ I d α ← β ⋅ det ⁡ I d α ← β ⇒

det ⁡ T β ← β = det ⁡ T α ← α ⋅ 1 ⇒

det ⁡ T β ← β = det ⁡ T α ← α

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #2

PUCRIO-P3-2014.1-2b

Verdadeiro ou Falso? Forneça uma justificativa para sua resposta.

Seja T : R 4 ⟶ R 4 uma projeção sobre a reta r ≔ 11 , - 1,7 , 4 = s p a n 11 , - 1,7 , 4 . Sejam T β a matriz de T numa base β de R 4 e P ∈ M 4 × 4 uma matriz invertível. Então, det ⁡ P T β P - 1 = 0 .

Passo 1

Vamos ver. O determinante det ⁡ P T β P - 1 = 0 , pode ser escrito através de usas propriedades como:

det ⁡ P ⋅ det ⁡ T β ⋅ det ⁡ P - 1 = det ⁡ P ⋅ det ⁡ T β ⋅ 1 det ⁡ P = det ⁡ T β

Assim, basta descobrir o determinante de T β . Também podemos usar o fato de que o determinante de matrizes em base diferentes são os mesmos!

Assim, vamos escolher uma outra base que nos agrada (e que realmente saibamos de fato), para ficar mais fácil de calcular.

Passo 2

Bom, agora existem alguns jeitos de calcular, um deles é achar a matriz no braço com uma base formada pela reta r e seu complemento ortogonal, mas isso vai dar muito trabalho até porque estamos no R 4 , então vamos nos deparar com 3 sistemas de 3 variáveis.

Uma solução mais prática é lembrar que o determinante dá zero quando possui uma linha/colunas de zeros (Use o Teorema de Laplace!).

Agora repare que se escolhermos a base formada pela reta e seu complemento ortogonal, quando montarmos a matriz T β vamos ter que calcular T dos vetores do complemento ortogonal (lembre-se de como calcular T β ), e sabemos que a imagem de um vetor de H ⊥ em uma projeção sobre H é zero!

Portanto, sempre teremos uma coluna ou linhas com zero, e assim o determinante é zero também!

Verdadeiro.

Resposta

Verdadeiro.

Exercício Resolvido #3

PUCRIO-P3-2014.2-2a

Para cada k real, considere a transformação T : R 3 ⟶ R 3 dada por:

T x , y , z = k x + 2 y ,   2 x + k y + 2 z ,   2 y + k z

Calcule em função de k , o determinante de T .

Dica: escolha uma base conveniente β de R 3 e determine T β .

Passo 1

Vamos seguir a dica do enunciado! Acredito que a base mais conveniente seja a canônica, então vamos calcular T ε , sendo:

ε = 1,0 , 0 , 0,1 , 0 , 0,0 , 1

T 1,0 , 0 = k , 2 , 0

T 0,1 , 0 = 2 ,   k ,   2

T 0,0 , 1 = 0 ,   2 ,   k

Logo,

T ε = k 2 0 2 k 2 0 2 k

Passo 2

Agora, basta calcular o determinante dessa matriz. Lembre-se que o determinante de uma matriz representada em uma base é igual ao determinante de todas as outras em outras bases! (Indo de uma base para a mesma base).

det ⁡ T ε = k 3 - 2 k - 2 k = k 3 - 4 k

Resposta

det ⁡ T ε = k 3 - 4 k

Exercício Resolvido #4

UFRJ-P4-2015.1-20

Seja Q o cubo no R 3 gerado pelos vetores da base canônica (o volume de Q é 1 ). Seja T : R 3 ⟶ R 3 a transformação linear associada a uma matriz P tal que P T P = 9 I , onde I é a matriz identidade 3 × 3 . Seja T ( Q ) a imagem de Q por T . O volume de T ( Q ) é:

a   9

b   3

c   27

d   1

Passo 1

Podemos interpretar o volume formado pelos vetores da coluna de uma matriz, como o determinante dessa matriz. Assim, vamos chamar a matriz que forma esse cubo de A , tal que:

A = 1 0 0 0 1 0 0 0 1

Ok, agora vamos achar o determinante da transformação (ou matriz P ) para saber o quanto o cubo aumenta. A única informação que temos é:

P T P = 9 I

E se aplicarmos o determinante dos dois lados:

det ⁡ P T P = det ⁡ 9 I ⇒

det ⁡ P T det ⁡ P = d e t ⁡ ( 9 I )

Passo 2

Agora muito cuidado ao calcular esses determinantes! Sabemos que o determinante da transposta é igual ao determinante da matriz original. E também que quando multiplicamos uma linha por um escalar, o determinante fica multiplicado por esse escalar. No caso a matriz I é multiplicado INTEIRAMENTE por 9 ou seja em todas as suas três linhas. Então, o determinante é multiplicado três vezes por 9 .

det ⁡ P 2 = 9 × 9 × 9 = 81 × 9 ∴

det ⁡ P = 81 × 9 ∴

det ⁡ P = 9 × 3 = 27

Assim sabemos que a T L amplia 27 vezes o volume do cubo e como o volume original era 1 , então o volume de T ( Q ) é 27 .

Resposta

Letra ( c )