Volume e Área com Determinante
Teoria
É isso mesmo que você leu no título, vamos aprender a calcular áreas e volumes com determinantes!!
Pois é, determinante serve pra tudo haha, normal você ficar assustado! Na verdade, essa foi uma das motivações da definição do determinante. O que acontece é que o determinante de uma matriz quadrada é uma generalização de área e volume! Vamos ver uns exemplos.
Determinante de matriz
O determinante de uma matriz pode ser definido como a área de um paralelogramo. Nesse caso, temos algo do tipo:
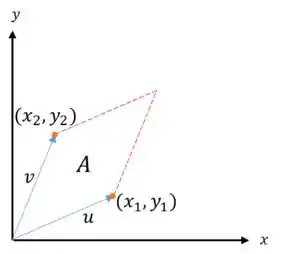
Para acharmos a área , basta jogarmos os vetores e nas colunas de uma matriz e calcular seu determinante! Então, teremos:
Note que, dependendo da ordem que você ordenar os vetores na matriz você pode encontrar uma área negativa. Portanto, para fins práticos de área e volume basta você ignorar esse sinal ;)
Beleza, e se tivéssemos a seguinte situação:
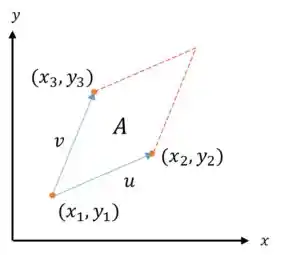
Cuidado que não podemos jogar as coordenadas e direto! Antes precisamos deslocar os vetores e para origem, dessa forma:
A área do paralelogramo é dada então por:
Por último, vamos ver como ficaria a área de um triângulo formado pelos vetores:
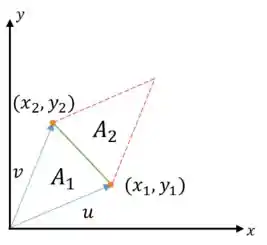
Essa imagem matou o problema né haha? Está claro que . Então basta acharmos a área do paralelogramo e dividirmos por :
Determinante de matriz
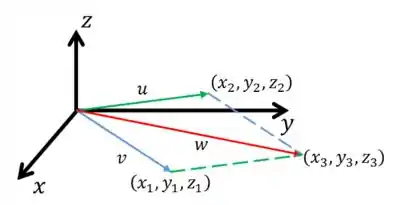
Finalmente vamos ao volume! A ideia é análoga. Se temos vetores no espaço e , gerando um paralelepípedo como o da figura abaixo:
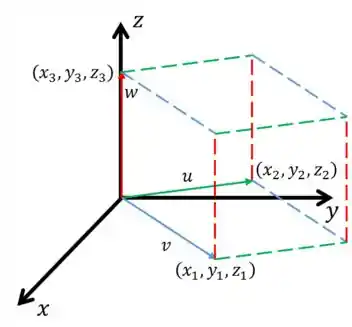
O volume do paralelepípedo gerado por esses vetores é dado por:
Da mesma forma, podemos ter um paralelepípedo deslocado. Nesse caso basta deslocarmos os vetores para a origem assim como fizemos no ;)
Volume e Área nulos
A parte mais legal de área e volume começa agora haha. Preparem-se para sentir aquela iluminação de quando tudo de repente se encaixa e passa a fazer sentido!
Bom, vamos pensar no . Lembra que o determinante de uma matriz com linhas ou colunas era zero? No vetores serem significa que os vetores estão no mesmo plano ou na mesma reta. Tipo assim:
E agora eu te pergunto qual o volume de um plano ou de uma reta? É zero obviamente!! Por isso que o determinante de matrizes será sempre !!! Se liga:
No vetores fazem parte da mesma reta. E a área de uma reta é zero! Fica difícil imaginar isso acima do já que não temos uma medida de “volume” para ou mais dimensões, mas o raciocínio seria análogo!
Determinante de matriz 3 × 3
Volume e Área nulos
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Sejam os vértices de um triangulo . Calcule a área desse triângulo.
Passo 1
Para fazer isso, precisamos pegar dois vetores que sejam os lados desse triângulo e depois botar esses vetores em colunas numa matriz e fazer o determinante.
Sendo assim, sejam dois vetores desse triângulo. Vamos tomar a origem como :
Seja
Passo 2
Agora basta achar o determinante da matriz:
E como sabemos que a área de um triangulo é:
Resposta
Exercício Resolvido #2
UFRJ-P3-2012.1
Determine o volume do paralelepípedo:
Passo 1
Determinar o volume do paralelepípedo é o mesmo que calcular o módulo do determinante da matriz cujas colunas são os vetores que se encontram num vértice qualquer.
Escolhendo o vértice , por exemplo. O vértice está ligado aos vértices , e .
Calculando os vetores nas arestas, fica assim:
Então o volume do paralelepípedo é dado por:
Passo 2
Usando a regra de Sarrus, temos:
Então:
Resposta
Letra
Exercício Resolvido #3
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 189 – Prob 6.6
Calcule o volume do paralelepípedo abaixo, cujos vértices são:
Passo 1
Primeiro vamos escolher um vértice para usar como origem. Tomando o como origem temos:
Então o volume do paralelepípedo é dado por:
Passo 2
Usando a regra de Sarrus, temos:
Então:
Resposta