Produto Vetorial
Produzido por Bruno PestanaTeoria
Cálculo do Produto Vetorial
Uma aplicação muito interessante para o determinante é o cálculo do produto vetorial. Como você já deve ter visto em física, o produto vetorial é um pouco diferente do produto interno.
O produto vetorial gera sempre um vetor perpendicular aos vetores multiplicados. Lembrando que ele é definido apenas no !!!
Notação: Denotamos o produto vetorial entre dois vetores como .
Sendo , o produto vetorial deles é: , veja a imagem abaixo:
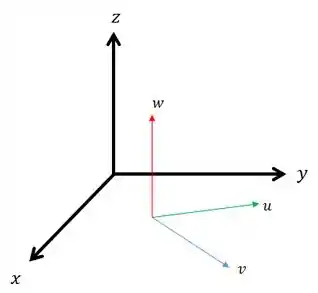
Mas como eu calculo esse terceiro vetor de fato??
Bom como o resultado do produto vetorial gera um vetor e não um número real, as coisas são um pouco diferentes, mas podemos usar determinante para calculá-lo.
Assim, sendo e , o nosso vetor será:
Aplicando qualquer um dos métodos para calcular determinantes, podemos ver que:
Sendo os vetores da base canônica do , isto é , nosso vetor terá as coordenadas do tipo:
Então basta jogar os vetores numa matriz e calcular o determinante? É basicamente isso, mas existem alguns cuidados antes de sair aplicando a fórmula!
Diferentemente do produto interno a ordem de produto vetorial importa! Ou seja, .
Repare que a primeira linha da matriz é composta pelos vetores unitários, a segunda linha é composta pelas coordenadas do primeiro vetor do produto e a última linha é composta pelas coordenadas do último vetor do produto.
Se trocássemos as duas últimas linhas de lugar teríamos ao invés de !!
Lembre-se também que quando trocamos duas linhas de lugar numa matriz, seu determinante muda de sinal!!! E é de fato isto que acontece!
Exemplo: Encontre o vetor perpendicular aos vetores . Basta fazer o produto vetorial entre os dois vetores:
Regra da mão direita
Agora imagina que você não precisa do vetor gerado pelo produto vetorial mas apenas da direção dele. Tem um jeito bem fácil de encontrar isso! Usando a regra da mão direita!
Mas como eu faço isso??? Bom existem vários jeitos de usar a regra da mão direita, mas vou tentar ensinar um jeito.
OBS: O nome é regra da MÃO DIREITA, porque só podemos utilizar a mão direita para fazer a regra!!!! NÃO use a mão esquerda!!! Pelo amor de Zeus!
Notação: Vamos ler , como vetorial .
Se queremos fazer , vamos fazer assim:
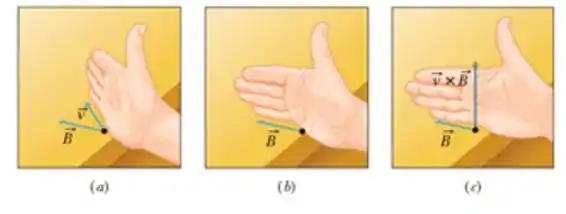
Para você fazer o produto vetorial siga essas três etapas:
Pegue a sua mão DIREITA, do jeito que está acima, e bota em cima do primeiro vetor, no caso é o , já que estamos fazendo vetorial .
Rode sua mão no sentido em que está o outro vetor COM A PALMA DA MÃO!! No nosso caso o . Vale ressaltar que você vai escolher o caminho mais curto entre os dois vetores!! Por ser um círculo, evidentemente você poderia girar sua palma para os dois lados, mas nós sempre optamos pela menor distância ok?
Veja para aonde está apontando o seu polegar. Este será o sentido do seu vetor perpendicular.
Vamos voltar ao nosso primeiro desenho:
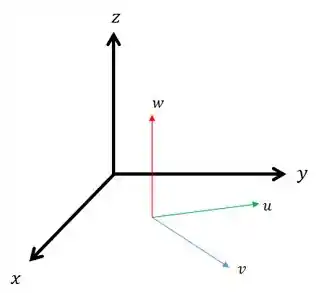
Repare que, se fizermos , como é vetorial , você pega a sua mão e bota em cima do vetor e bota sua palma virada para o vetor e gira até ele. Repara que se você fizer isso seu polegar ficará pra baixo né? Pois o menor caminho de você girar a sua palma até o vetor é com o polegar virado para baixo. Sacou?
Propriedades do Produto Vetorial
Bom, antes de encerrarmos vamos ver algumas propriedades do produto vetorial ;)
é perpendicular a e
Era só isso que tinha pra falar mesmo haha.
Regra da mão direita
Propriedades do Produto Vetorial
Exercícios Resolvidos
Exercício Resolvido #1
Lista de monitoria 1 para a P3, exercício 4, Álgebra Linear I, PUC-rio.
Sejam e . Calcule uma base para o complemento ortogonal de , usando o produto vetorial. Em seguida determine uma base ortogonal de tal que .
Passo 1
Primeiramente, como estamos no , e sabemos que é um plano, seu complemento ortogonal é uma reta. Assim, basta que façamos o produto vetorial dos geradores de . Isso irá gerar um vetor perpendicular a esses dois.
Passo 2
Agora, falta calcular uma base ortogonal de . Uma coisa que podemos fazer é tomar, , e , pois já sabemos que eles serão paralelos (um pertence ao complemento ortogonal do outro!). Por fim, fazemos . Olhe a figura:
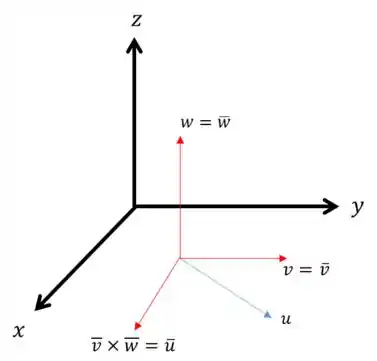
Repare que ainda pertencem ao mesmo plano de , e como eles vão ser ortogonais entre si, eles vao ser também. E, com isso, podemos dizer que .
Passo 3
Temos que:
Vamos então calcular .
Assim uma base ortogonal para o é:
E podemos dizer também que:
Resposta
Base para o :