Determinantes em Blocos
Produzido por Bruno PestanaTeoria
Determinantes em Blocos
Vou mostrar agora mais um método para o cálculo de determinantes. É um pouco parecido com o determinante de matrizes triangulares, só que mais geral.
Primeiramente, o quer dizer Matrizes em blocos?
Bom, vamos supor uma matriz assim:
Sendo matrizes quadradas. Ou seja, as matrizes da diagonal devem ser quadradas.
Pera deixa eu ver se eu entendi, então temos uma matriz com varias outras matriz quadradas dentro dela???? Sim, e por isso serão matrizes um tanto grandes.
E o ali em cima? Ele também é um bloco de zeros, e não o número zero em si??? Não necessariamente!!! O ali em cima é um conjunto de zeros, pode ser uma linha de dois, três quatro zeros! Pode ser também um quadradinho que nem as matrizes mas não é necessário! Vou dar uns exemplos pra você:
Essa é uma possível matriz em blocos

Primeiramente repare que não temos um quadrado de zeros! O que nós temos é uma linha de três zeros! Mas por que isso funciona?
Nós temos que separar a matriz de um jeito que fique igual aos três jeitos anteriores. Olha a imagem abaixo:

Esse é exatamente o caso:
Hã??? Como assim??
Ué temos que achar matrizes quadradas né?? Então, só fazer:
Pera aiiii!!! A matriz é quadrada, tudo normal. Mas e a outra matriz ??? Só tem um elemento!
Isso é verdade, mas não deixa de ser uma matriz quadrada, repare que ela é e então satisfaz as condições que estipulamos antes.
E esta matriz?
Bom, vamos tentar separar em duas matrizes quadradas!
Viu que não deu pra separar em duas matrizes quadradas?
Mas por que isso tudo é importante???
Porque o determinante dessas matrizes é fácil de calcular!
Se você reparar na forma dessas matrizes verão que se assemelham muito à matrizes triangulares! Elas são chamadas matrizes bloco-triangulares. Não por acaso, o determinante dessas matrizes vai ser sempre da forma:
Assim, para calcular o determinante lá da matriz da letra :

É só fazer:
Sendo:
Repare que a primeira coluna multiplicada por , somada a segunda dá a terceira:
Como a matriz é , só possui um único elemento e o determinante é ele mesmo.
Logo:
Vale ressaltar que, apesar de ser a forma mais comum, você não precisa separá-la em apenas blocos! O importante é transformá-la em uma matriz bloco-triangular. Veja o exemplo abaixo:

Essa matriz em blocos é dada por:
Que é uma matriz triangular onde,
Portanto, temos que seu determinante vale:
Exercícios Resolvidos
Exercício Resolvido #1
Livro Curso de Álgebra Linear Fundamentos e Aplicações, Marco Cabral e Paulo Goldfeld, página 189 Problema 6.5
Divida em blocos para calcular o determinante das matrizes abaixo (trocando linhas ou colunas de lugar se necessário).
Passo 1
Temos que dividir a matriz na forma:
De modo que no lugar do ou tenha pelo menos um bloco de zeros. Assim, podemos ver que na letra , podemos tomar E assim podemos aplicar a propriedade do determinante de matriz em blocos!
Como:
Podemos calcular o determinante da matriz original:
Passo 2
Bom, essa matriz já é um pouco mais difícil de calcular, pois não se enquadra nestes tipos: . O bloco de zeros está no lugar das matrizes e assim não dá pra aplicar a propriedade que queremos. Entretanto podemos trocar a coluna com a coluna e a coluna com a coluna , lembrando que o determinante muda de sinal cada vez que fazemos isso e como fizemos isso duas vezes o sinal volta a ser o original.
Agora sim temos uma matriz do tipo e podemos aplicar as propriedades! Mas antes, vamos separar quem são as matrizes :
Assim fica fácil de calcular o determinante da matriz original:
Passo 3
Dessa vez não temos um grupo quadradinho de zeros, mas lembre-se que não precisamos disso! Basta dividirmos um grupo de zeros com a matriz quadradas:
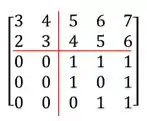
Assim, basta tomar:
Logo o determinante da nossa matriz é:
Resposta
Exercício Resolvido #2
Elaboração própria
Calcule o determinante da matriz abaixo.
Passo 1
Essa matriz parece muito grande né? Bom realmente ela é, mas podemos dar um jeito nisso. Repare que ela tem muitos zeros na e coluna, porém isso não é nada vantajoso para nós, pois precisamos de matrizes desse jeito:
Para podemos calcular o determinante por matrizes em blocos. Assim o que podemos fazer é trocar as duas últimas colunas com as duas primeiras:
Lembrando que como trocamos duas colunas o sinal do determinante não altera.
Passo 2
Agora sim podemos separar em blocos essa matriz:
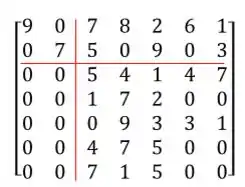
Tomando:
E assim:
Bom, chegamos de novo em uma matriz grande. Do jeito que ela está, não podemos dividir em blocos de zero do jeito que gostaríamos, o que podemos fazer é trocar a terceira linha com a segunda linha:
Passo 3
Agora vamos trocar a coluna com a e a com a :
E agora podemos separar a matriz em blocos:
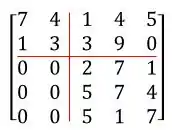
Assim seu determinante vai ficar:
Sendo:
E assim podemos finalmente calcular o determinante da nossa matriz :
Passo 4
Vamos começar calculando o determinante de :