Teoria
Para começar a aquecer os motores e ter uma “dimensão” (haha) do que é esse tópico, vamos olhar esse conjunto abaixo:
Bom, de cara já podemos perceber que esse conjunto não possui muitos geradores. Podemos ver que os dois últimos são dos demais. Assim, poderíamos restringir os geradores apenas aos vetores
Assim podemos definir esses vetores como uma base para o conjunto .
Poderíamos ter notado que há vetores “demais” no conjunto, pois, se esses vetores fossem , teríamos um espaço gerado por vetores.
Mas eles pertencem ao , que é gerado por apenas vetores! E não podemos ter um espaço gerado “maior” que o próprio espaço em que os vetores geradores estão contidos! Não faria sentido, né?
Vamos formalizar essa noção de “tamanho”: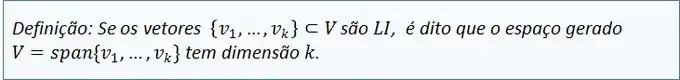
OBS: Podemos entender também que a dimensão de um conjunto ou espaço gerado é igual ao número de vetores que geram esse espaço ou conjunto.
Notação: .
Por exemplo, o é formado por vetores , logo ele tem dimensão .
O conjunto das matrizes , possui dimensão , pois:
E a dimensão de , polinômios de no máximo de grau 2 é:
Então, o que eu quis dizer ali em cima é:
“Não podemos ter um espaço gerado com dimensão maior do que o próprio espaço em que o nosso espaço gerado está contido”
No nosso caso ali, temos vetores geradores do . Como a dimensão do é , então a dimensão máxima de qualquer conjunto contido no é e fim de papo.
No exemplo acima podemos ver que , pois possui dois geradores , e, portanto, trata-se de um plano! (Confira!) Uma coisa importante sobre planos e retas é:
- um plano sempre tem dimensão igual a , pois possui sempre geradores ;
- uma reta sempre tem dimensão igual a , pois possui sempre gerador .
Polinômios
Tenho uma pergunta pra vocês. Esse conjunto aqui em baixo é uma base do ?
Se você disse sim, você caiu numa das maiores pegadinhas da álgebra! Mas fica tranquilo que muita gente erra isso quando está aprendendo mesmo!
De fato, esse conjunto é uma base do plano no . O problema é que o plano no e o não são a mesma coisa! Isso porque o contêm vetores com DUAS coordenadas! Então o conjunto NUNCA poderia gerar o já que ele tem vetores de coordenadas.
De forma geral isso acontece porque para . Ou seja, nesse caso o não contém o , então um conjunto de vetores do nunca poderia gerar o !
Show de bola, próxima pergunta:
O que acham? está contido em ? Ahh, isso parece meio óbvio, é que nem o e o né?? Ai que você se engana, jovem padawan. Vetores de coordendas não conseguem gerar vetores de coordenadas. Então nunca que uma base do vai gerar o !! Mas para polinômios isso não é necessariamente verdade!!
Se pegarmos uma base para ela consegue gerar polinômios de (apesar de uma base de não ser uma base de ). Repare, no espaço gerado de :
Então se zerarmos a terceira coordenada, ficamos apenas com:
Que são todos os polinômios de no máximo grau . Sendo assim, sempre um espaço de grau menor vai estar contido no de grau maior para polinômios!
Essa diferença acontece porque o é formado por todos os vetores de coordenadas. Já o é formado por todos os polinômios de grau igual ou menor que . Esse “menor” na definição é que muda o raciocínio! Então fica ligado porque os professores adoram explorar essa diferença nas provas haha.
Resumindo:
para
para
Repare que para , é verdade, pois todo conjunto é subconjunto dele mesmo.
Agora, vamos pros exercícios!
Polinômios
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Faça o que se pede
a) Encontre uma base para:
Além disso, diga qual a dimensão de .
b) O conjunto:
é linearmente independente? Calcule também .
c) Dê uma base e uma dimensão para :
Passo 1
a) Antes de tudo, vamos tentar achar os vetores que são dos outros, pois uma base possui apenas vetores (lembrar a definição!).
Olhando para o espaço gerado, podemos descartar o vetor nulo, que é uma de qualquer vetor.
Podemos verificar que o vetor pode ser escrito como
e também pode ser eliminado. Logo, nos resta apenas:
Passo 2
Podemos observar também que
e vamos descartar o vetor também.
Assim sobrou apenas:
Esses vetores ai em cima são , pois um não é uma do outro. Na dúvida, aplique a definição e verifique (ache coeficientes iguais a zero).
Encontramos
Como a base possui vetores, temos .
Passo 3
Letra b) Bom, se queremos verificar se aquele conjunto é , vamos fazer uma entre eles:
Após desenvolver, basta apenas agrupar os termos em , já que sabemos que este conjunto é . Assim, igualamos seus coeficientes a zero.
Passo 4
Substituindo as equações e na , temos:
Portanto podemos concluir que:
Então, se colocarmos teremos zero, ou seja, existe uma combinação linear dando zero sem ser a trivial. O que isso nos diz? Que os vetores são LD!
Beleza agora que sabemos que o conjunto é LD, vamos ver qual ou quais vetores podem ser escrito como CL dos demais. Dessa forma, saberemos quais podem ser descartados por serem redundantes e assim teremos nossa base!
Nossa equação principal fica assim:
Dividindo tudo por , já que como são ,:
Passo 5
E assim vemos que podemos descartar . Mas isso não torna o novo conjunto
. Precisamos verificar isso de novo. Uma dica para não ter tanto trabalho é aproveitar as equações já feitas e apenas remover o delas.
Tomando pela equação :
Somando as duas vemos que:
Portanto, sim, o novo conjunto é e a dimensão é 3.
Passo 6
Letra c) Primeiramente, vamos verificar se o conjunto é , mas, em vez de usarmos a definição podemos ter um pouco menos de trabalho e usar o teorema vendo se alguma matriz é uma das demais. Sempre tente fazer isso antes de aplicar a definição a não ser que peçam para você provar, é claro.
Repare que, para a quarta matriz, 2. Logo, podemos descartar esta quarta matriz.
Outra coisa que podemos ver é que a terceira matriz é a soma da primeira com a segunda. Assim podemos eliminar já as duas últimas.
Passo 7
Repare que as duas que sobraram
são , pois uma possui um zero no terceiro elemento, e a outra zero no quarto elemento, logo uma não consegue gerar a outra.
Assim uma possível base é e .
Resposta
a) , .
b) Não. .
c) Base e .
Exercício Resolvido #2
Combinação Linear, Base e Dimensão
Dizemos que duas matrizes comutam se satisfazem . Considere o conjunto de todas as matrizes que comutam com
Considere agora o caso particular das matrizes e .
e) Calcule a dimensão de .
Passo 1
Letra e)
Seja
Como temos a matriz dessa vez, vamos aplicar as condições de e achar a de fato:
Passo 2
Substituindo os valores na :
Logo,
Como achamos duas matrizes , então
Resposta
Ei, a resposta está no passo a passo :)