Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Núcleo e Imagem de uma TL

Ver Todos os Exercícios

Teoria

Já demos uma olhada no que é uma T L . Então agora vamos nos aprofundar em duas coisas chamadas Núcleo e Imagem. Mas, primeiro vamos começar com o Núcleo.

Núcleo de uma TL

Lembra de quando estudávamos funções, onde um elemento era uma raiz se zerasse a função? Tipo, 1 é raiz da função f x = x - 1 porque f 1 = 0 .

Uma coisa importante que temos que lembrar disso é que as raízes dessa função f ( x ) pertencem ao seu domínio. Já o zero gerado está no contra-domínio!

O Núcleo de uma T L é bem parecido com isso. Ele é o conjunto dos elementos do domínio (sejam eles vetores, matrizes ou polinômios) que zeram a T L . A definição é a seguinte:

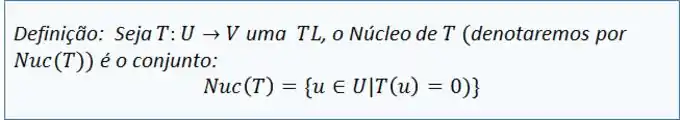
Repetindo, os geradores do núcleo sempre pertencem ao domínio da T L !! Veja na definição do conjunto N u c ( T ) que todos os vetores desse conjunto ∈ U , que é o domínio da T L .

To batendo muito nessa tecla, mas se reclamar bato mais ainda haha, porque é muito importante galera. Tem que tá no sangue.

Tá, agora que todo mundo entendeu a definição vamos aprender a achar essa bagaça.

Por exemplo, temos essa simpática T L :

T : R 3 → R 2

T x , y , z = ( x - 2 y + z , 2 x + y + z )

Para acharmos os geradores do núcleo é só igualarmos a T L ao elemento nulo do contra-domínio.

Vale ressaltar duas coisas importantes aqui. Primeiro, o elemento nulo não é necessariamente o zero, lembra galera? Segundo, você iguala ao vetor nulo do contra-domínio. Até porque não faria sentido igualar à um vetor fora do espaço que essa T L leva né haha. Continuando:

T x , y , z = x - 2 y + z , 2 x + y + z = 0,0

x - 2 y + z = 0     2 x + y + z = 0 ( I ) ( I I )

De ( I ) :

z = 2 y - x

Substituindo em I I :

2 x + y + z = 0

2 x + y + 2 y - x = 0

x = - 3 y   ( I I I )

I I I em I :

x - 2 y + z = 0

- 3 y - 2 y + z = 0

z = 5 y

Sendo assim, os geradores do núcleo são o conjunto dos vetores ( x , y , z ) que tem x = - 3 y e z = 5 y . Então eles vão ter essa cara:

x , y , z = - 3 y , y , 5 y = y ( - 3,1 , 5 )

Loooogo, N u c T = s p a n - 3,1 , 5 ou N u c T = 〈 ( - 3,1 , 5 ) 〉 .

Opa, lembram que os elementos do Núcleo pertencem ao domínio (ai de vocês se não lembrarem!)? Então, note que o vetor genérico que a gente arrumou tem três coordenadas! Então ele é do R 3 né, que é o domínio da nossa T L ;)

Vale comentar mais algumas coisas:

Não é muito difícil de vermos que o núcleo de uma T L será sempre um espaço vetorial do domínio dela (porque ele faz parte do domínio!!!). Se duvidar de mim pode provar aí que você já sabe fazer isso haha. Então:

Nesse exemplo que eu dei o núcleo tinha dimensão 1 (é o espaço gerado por um único vetor). Então, podíamos dizer que a Nulidade dessa transformação T é 1 . A Nulidade de uma transformação linear T é a dimensão do seu núcleo: dim ⁡ N u c T .

Ah, e não esquece:

Imagem de uma TL

Além do Núcleo, existe um outro espaço vetorial muito importante relacionado a uma transformação: a imagem. A imagem de uma transformação são todos os elementos transformados a partir do domínio de uma T L .

Ou seja, são todos os elementos do contra domínio que a T L gera. Mais formalmente:

Repare que os elementos da imagem sempre, SEMPRE, pertence ao contra domínio, pois são os elementos transformados T ( u ) . Assim, I m T ⊂ V . Isso aí, vou ficar batendo nessa tecla igual fiz com o núcleo haha.

Beleza, mas como eu acho qual é essa imagem? E quais são os geradores dela?

Vamos pegar, por exemplo, essa outra transformação

T : R 2 → R 3 T x , y = ( x + y , x - y , 2 x )

Primeiro vamos desmembrar a fórmula da T L . Teremos:

x + y , x - y , 2 x = x 1,1 , 2 + y ( 1 , - 1,0 )

Assim, I m T = s p a n 1,1 , 2 , 1 - 1,0 = 1,1 , 2 , 1 , - 1,0

Oi? Só isso?! Sim, só isso haha. Mamatinha.

Note que os vetores da imagem possuem 3 coordenadas! E temos que D o m T = R 2 e o C D T = R 3 . Loooooogo (isso aí, vou falar de novo), a imagem está no contra domínio!

Assim como quando falamos de núcleo, vale comentar algumas coisas:

A imagem de uma T L também será sempre um subespaço vetorial do contra domínio da T L . Então:

Também temos um nome especial para a dimensão da imagem. O Posto de uma transformação linear T é a dimensão da sua imagem dim ⁡ I m T .

Obs: O termo nulidade não é tão usado, mas o termo posto é muito comum então vale a pena gravar.

Por último, mas não menos importante:

Imagem de uma TL

Exercícios Resolvidos

Exercício Resolvido #1

Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 126 – Fix. 4.7

Seja T : V → W uma T L . A definição de N u c ( T ) é:

a   { w ∈ W | T 0 = w }

b   { w ∈ W | T w = 0 }

c   { v ∈ V | T v = 0 }

d   { v ∈ V | T 0 = v }

Passo 1

Bom, o que nós sabemos sobre o núcleo de uma T L ? Sabemos que o núcleo é composto por todos os elementos que a T L leva no zero e, é claro, que o núcleo faz parte do domínio da T L .

Po, o domínio dessa T L é V . Logo, os vetores do núcleo também devem pertencer a V . Isso elimina as duas primeiras alternativas.

E para um vetor v pertencer ao núcleo, a T L , quando aplicada nele, deve dar zero, ou seja:

T v = 0

Sendo assim, a alternativa correta é a c .

Resposta

Letra c

Exercício Resolvido #2

Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 126 – Fix 4.7

Seja T : V → W uma T L . A definição de I m ( T ) é:

a   { w ∈ W | w = T v   p a r a   a l g u m   v ∈ V }

b   { w ∈ W | v = T w   p a r a   a l g u m   w ∈ W }

c   { v ∈ V | w = T v   p a r a   a l g u m   v ∈ V }

d   { v ∈ V | v = T w   p a r a   a l g u m   w ∈ W }

Passo 1

Bom, o que nós sabemos sobre a imagem de uma T L ? Sabemos que a imagem é composta por todos os elementos que a T L pode gerar e, é claro, que a imagem faz parte do contra domínio da T L .

Po, o contra domínio dessa T L é W . Logo, os vetores da imagem devem pertencer a W . Isso elimina as duas últimas alternativas.

E a T L tem que levar algum vetor do domínio v ∈ V nesse vetor da imagem w ∈ W . Logo, temos que para todo w ∈ W deve existir um v ∈ V tal que:

T v = w

Sendo assim, a alternativa correta é a a .

Resposta

Letra a

Exercício Resolvido #3

Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 128 – Prob 4.5

Considere T 1 ,   T 2 : R 3 → R 2 definidas por T 1 x , y , z = ( x - y + z , 2 x - y ) e T 2 x , y , z = ( 3 x - 2 y + z , x - z ) . Determine uma base para N u c ( T 1 ) ∩ N u c ( T 2 ) .

Passo 1

Beleza, antes de qualquer coisa temos que achar o núcleo das T L s né. Então vamos lá. Igualando T 1 ao elemento nulo do R 2 :

T 1 x , y , z = x - y + z , 2 x - y = ( 0,0 )

Daí:

x - y + z = 0 2 x - y = 0 1 2

De ( 2 ) temos que:

2 x = y

Substituindo em 1 :

x - 2 x + z = 0

z = x

Sendo assim os vetores do N u c ( T 1 ) são da forma:

x , 2 x , x = x ( 1,2 , 1 )

Ou seja,

N u c T 1 = 1,2 , 1

Passo 2

Agora igualando T 2 ao elemento nulo do R 2 :

T 2 x , y , z = 3 x - 2 y + z , x - z = ( 0,0 )

Dessa igualdade tiramos:

3 x - 2 y + z = 0 x - z = 0 1 2

De 2 :

x = z

Substituindo em 1 :

3 x - 2 y + x = 0

4 x = 2 y

2 x = y

Então, os vetores de N u c ( T 2 ) tem essa cara:

x , 2 x , x = x ( 1,2 , 1 )

Logo,

N u c T 2 = 1,2 , 1

Passo 3

Bom, do resultado que obtivemos está claro que N u c ( T 1 ) e N u c ( T 2 ) são o mesmo subespaço! Como a interseção entre dois espaços iguais é o próprio espaço, teremos que:

N u c T 1 ∩ N u c T 2 = N u c T 1 = N u c T 2 = 1,2 , 1

Então, uma base para N u c ( T 1 ) ∩ N u c ( T 2 ) seria 1,2 , 1

Resposta

1 2 1

Exercício Resolvido #4

Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 127 – Fix 4.14

Considere D 2 : P 3 → P 3 definida por D 2 f = f ' ' (duas derivadas). Determine se fazem parte do N u c D 2 :

a   3 x 3 + x 2

b   3 x - 4

c   x 2

d   5

Passo 1

Primeiro, qual o domínio e o contra domínio dessa T L ? Ela pega vetores do P 3 e leva em vetores do P 3 . Logo, ambos são o P 3 . Lembrando que P 3 é o espaço dos polinômios de terceiro grau ou menor.

Deixei o “ou menor” em negrito porque temos que ter cuidado pra não eliminarmos as letras b , c e d só porque não são de terceiro grau. Elas fazem parte de P 3 !!

Dito, isso, vamos testar letra por letra.

Passo 2

a Aplicando a T L ao polinômio dado:

D 2 3 x 3 + x 2 = 3 x 3 + x 2 ' ' = 9 x 2 + 2 x ' = 18 x + 2

Bom, 18 x + 2 claramente não é igual ao elemento nulo do contra domínio: ( 0 x 3 + 0 x 2 + 0 x + 0 ) .

Logo, ele não faz parte do N u c ( D 2 ) .

Passo 3

b Aplicando a T L :

D 2 3 x - 4 = 3 x - 4 ' ' = 3 ' = 0

Opa, a transformação levou o polinômio 3 x - 4 em 0 . Logo, ele faz parte do N u c D 2 .

Passo 4

c Aplicando a T L ao polinômio dado:

D 2 x 2 = x 2 ' ' = 2 x ' = 2

Novamente 2 ≠ 0 . Logo, x 2 não faz parte do N u c ( D 2 ) .

Passo 5

d Por último:

D 2 5 = 5 ' ' = 0 ' = 0

Como D 2 5 = 0 , ele faz parte do N u c ( D 2 ) .

Resposta

b e d fazem parte do N u c ( D 2 ) .

Exercício Resolvido #5

Alfredo Steinbruch e Paulo Winterle, Álgebra Linear, 2ª ed., São Paulo, Pearson, 1987, pp. 215. 14 até 21

Para as transformações abaixo determine a imagem, uma base para esse subespaço e sua dimensão:

a   T : R 2 → R 2 ,   T x , y = ( 3 x - y , - 3 x + y )

b   T : R 2 → R 3 ,   T x , y = ( x + y , x , 2 y )

c   T : R 2 → R 2 ,   T x , y = ( x - 2 y , x + y )

d   T : R 3 → R 2 ,   T x , y , z = x + 2 y - z , 2 x - y + z

e   T : R 3 → R 3 ,   T x , y , z = ( x - y - 2 z , - x + 2 y + z , x - 3 z )

f   T : R 3 → R 3 ,   T x , y , z = ( x - 3 y , x - z , z - x )

g   T : P 1 → R 3 ,   T a t + b = ( a , 2 a , a - b )

h   T : M 2 × 2 → R 2 ,   T a b c d = ( a - b , a + b )

Passo 1

Caraca, perderam a linha com essas letras todas né? Tenha coragem que esse tipo só tem dois exercícios então tem que fazer valer haha.

Primeiro vamos lembrar como achar a imagem né. É só “desmembrar” a fórmula da T L lembra? Escrevemos ela em termos de x , y e z .

Obs: É interessante reparar que os vetores da imagem terão sempre o formato do contra domínio da T L ;)

Passo 2

a T x , y = 3 x - y , - 3 x + y = x 3 , - 3 + y - 1,1

Assim,

I m T = 3 , - 3 , - 1,1

Opa, mas ainda não temos uma base né? Nesse caso está fácil de ver que os vetores que achamos são L D . Então, uma base para a imagem poderia ser:

- 1,1

Como a base tem um elemento, a dimensão da imagem é 1 .

Passo 3

b x , y = x + y , x , 2 y = x 1,1 , 0 + y ( 1,0 , 2 )

Logo,

I m T = s p a n 1,1 , 0 , 1,0 , 2

Como os vetores são L I , uma base para a imagem é:

1 1 0 , 1 0 2

A base tem dois elementos, então o posto é 2 .

Passo 4

c   T x , y = x - 2 y , x + y = x 1,1 + y ( - 2,1 )

Dessa forma,

I m T = 1,1 , - 2,1 = R 2

Repare que como o contra domínio é o R 2 , como a imagem é gerada por 2 vetores L I então ela equivale ao próprio R 2 . Temos como base da imagem:

1,1 , - 2,1

Dois elementos na base implicam que dim ⁡ I m T = 2 .

Passo 5

d   T x , y , z = x + 2 y - z , 2 x - y + z = x 1,2 + y 2 , - 1 + z - 1,1

Sendo assim,

I m T = s p a n 1,2 , 2 , - 1 , - 1,1 = R 2

Bom, temos três elementos do R 2 , então eles obviamente não formam uma base. No entanto, dando uma olhada rápida dá pra perceber que são todos L I um a um entre si, por isso, podemos garantir que I m T = R 2 .

Então é só escolher dois vetores quaisquer, que eles serão uma base xD. Vou pegar os dois primeiros:

1 2 , 2 - 1

Logo, a imagem tem dimensão 2 .

Passo 6

e   T x , y , z = x - y - 2 z , - x + 2 y + z , x - 3 z = x 1 , - 1,1 + y - 1,2 , 0 + z - 2,1 , - 3

Então,

I m T = 1 , - 1,1 , - 1,2 , 0 , ( - 2,1 , - 3 )

Opa, e agora? L D ou L I ? Tá mais complicado de ver né? Sem problemas, uma escalonada rápida resolve o problema:

1 - 1 1 - 1 2 0 - 2 1 - 3 → L 2 ← L 2 + L 1 L 3 ← L 3 + 2 L 1 1 - 1 1 0 1 1 0 - 1 - 1 → L 3 ← L 3 + L 2 1 - 1 1 0 1 1 0 0 0

Chegamos à conclusão que são L D . Lembrando que o espaço gerado pelos vetores que obtemos do escalonamento é o mesmo espaço gerado por aqueles três vetores do começo, uma base para a imagem é:

1 - 1 1 , 0 1 1

A base tem dois elementos então o posto da T L é 2 .

Passo 7

f   T x , y , z = x - 3 y , x - z , z - x = x 1,1 , - 1 + y - 3,0 , 0 + z 0 , - 1,1

Logo,

I m T = s p a n 1,1 , - 1 , - 3,0 , 0 , 0 , - 1,1

Esse daí dá pra perceber que é L D né? Se não viu eu te dou uma ajuda:

1,1 , - 1 = - 1 3 - 3,0 , 0 - 0 , - 1,1

Foi? Beleza então. Podemos descartar o primeiro vetor e tomar como base para a imagem:

- 3 0 0 , 0 - 1 1

Base de dois elementos, então dim ⁡ I m T = 2 .

Passo 8

g   T a t + b = a , 2 a , a - b = a 1,2 , 1 + b 0,0 , - 1

Daí,

I m T = 1,2 , 1 , 0,0 , - 1

Como são L I , eles formam uma base para a imagem:

1,2 , 1 , 0,0 , - 1

Dois elementos na base, então a imagem tem dimensão 2 .

Passo 9

h   T a b c d = a - b , a + b = a 1,1 + b - 1,1

Desse modo,

I m T = s p a n 1,1 , - 1,1 = R 2

São L I , então uma base para a imagem é:

1,1 , - 1,1

O posto da T L vale 2 pois possui dois elementos em sua base.

UFAAAA! Acabamos, nem foi tão ruim né? :P

Resposta

a I m T = 3 , - 3 , - 1,1

b a s e = - 1,1

dim ⁡ I m T = 1

b I m T = s p a n 1,1 , 0 , 1,0 , 2

b a s e = 1 1 0 , 1 0 2

dim ⁡ I m T = 2

c I m T = R 2

b a s e = 1,1 , - 2,1

dim ⁡ I m T = 2

d I m T = R 2

b a s e = 1 2 , 2 - 1

dim ⁡ I m T = 2

e I m T = 1 , - 1,1 , - 1,2 , 0 , ( - 2,1 , - 3 )

b a s e = 1 - 1 1 , 0 1 1

dim ⁡ I m T = 2

f I m T = s p a n 1,1 , - 1 , - 3,0 , 0 , 0 , - 1,1

b a s e = - 3 0 0 , 0 - 1 1

dim ⁡ I m T = 2

g I m T = 1,2 , 1 , 0,0 , - 1

b a s e = 1,2 , 1 , 0,0 , - 1

dim ⁡ I m T = 2

h I m T = R 2

b a s e = 1,1 , - 1,1

dim ⁡ I m T = 2

Exercício Resolvido #6

Elaboração Própria

Dado v = x 0 y 0 z 0 ∈ M 3 × 1 fixo, a transformação T : M 3 × 3 ⟶ M 3 × 1 dada por T A = A v é linear. Determine uma base do núcleo de T quando v = 1 0 - 1 .

Passo 1

Para achar uma base para o núcleo, primeiramente, devemos fazer:

T A = A v = 0

Desenvolvendo:

a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9 1 0 - 1 = 0 ⇒

a 1 - a 3 = 0 ⇒ a 1 = a 3 a 4 - a 6 = 0 ⇒ a 4 = a 6 a 7 - a 9 = 0 ⇒ a 7 = a 9

Substituindo num elemento genérico do domínio temos:

a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9 = a 1 a 2 a 1 a 4 a 5 a 4 a 7 a 8 a 7 =

= a 1 1 0 1 0 0 0 0 0 0 + a 2 0 1 0 0 0 0 0 0 0 + a 4 0 0 0 1 0 1 0 0 0

+ a 5 0 0 0 0 1 0 0 0 0 + a 7 0 0 0 0 0 0 1 0 1 + a 8 0 0 0 0 0 0 0 1 0

E assim uma possível base para o núcleo é:

β = 1 0 1 0 0 0 0 0 0 ,   0 1 0 0 0 0 0 0 0 ,   0 0 0 1 0 1 0 0 0 ,   0 0 0 0 1 0 0 0 0 ,   0 0 0 0 0 0 1 0 1 ,   0 0 0 0 0 0 0 1 0

Resposta

Base para o núcleo: β = 1 0 1 0 0 0 0 0 0 ,   0 1 0 0 0 0 0 0 0 ,   0 0 0 1 0 1 0 0 0 ,   0 0 0 0 1 0 0 0 0 ,   0 0 0 0 0 0 1 0 1 ,   0 0 0 0 0 0 0 1 0

Exercícios de Livros Relacionados

(Requer cálculo) Seja V o espaço vetorial das funções reais com derivadas continuas de todas as ordens no intervalo - ∞ ,∞ e W = F ( - ∞ ,∞ ) o espaço vetorial de todas as funções reais definidas em (
Se A for uma matriz m × n e se o sistema linear A x = b for consistente com qualquer vetor b em R m , o que pode ser dito sobre a imagem de T A : R n → R m ?
Sejam A e B matrizes mxpepxn , respectivamente. Seja C = A B . Mostre que:f) Se as colunas de B são linearmente dependentes, então as colunas de C também são linearmente dependentes.