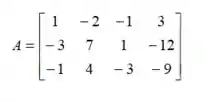Exercícios de Núcleo e Imagem de uma TL - Lista de Exercícios Resolvida

Seja uma . A definição de é:

Seja uma . A definição de é:

Considere definidas por e . Determine uma base para .

Considere definida por (duas derivadas). Determine se fazem parte do

Para as transformações abaixo determine a imagem, uma base para esse subespaço e sua dimensão:

Dado fixo, a transformação dada por é linear. Determine uma base do núcleo de quando .

Seja uma transformação linear, onde é um espaço vetorial de dimensão finita. Considere as seguintes aformações:

1. Se é linearmente dependente, então é linearmente dependente.
2. Se é linearmente dependente, então é linearmente dependente.

Então:

é verdadeira e é falsa

é falsa e é verdadeira

ambas são falsas

ambas são verdadeiras

05) Seja a transformação linear definida por

para qualquer . Assinale a alternativa correta:

a)

b) se forem tais que pertença ao núcleo de , então será igual a ;

c) se forem tais que pertença ao núcleo de , então será igual a

d) é bijetora;

e)

Considere a função definida por:

(Observe que é a transformação que deriva o polinômio)

Determine uma base para o núcleo de e uma base para a imagem de

Considere as transformações lineares A, B, C: cujas matrizes na base canônica são, respectivamente:

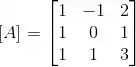
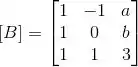
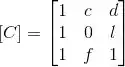
(a) Determine uma base do espaço imagem de A (ou, equivalentemente, o espaço coluna da matriz ).

(b) Determine a e b para que a imagem de B (ou, equivalentemente, o espaço coluna da matriz ) seja um plano.

(c) Determine c, d, l e f para que a imagem de C (ou, equivalentemente, o espaço coluna da matriz ) seja uma reta.

Considere o sistema:

Seu conjunto-solução é igual a translação de um sub-espaço de dimensão:

1. 3
2. 2
3. 4
4. 1

Assinale abaixo a transformação linear cujo núcleo é dado pelo conjunto-solução de e cuja imagem é dada pelo conjunto solução de .

Considere os vetores de , cujas coordenadas na base canônica são:

E as matrizes:

1. Determine se é uma base de .
2. Determine se é uma base de
3. Determine o posto de .
4. Determine o posto de .
5. Considere os vetores

E o espaço gerado por estes vetores

Determine uma base e a dimensão de .

(Nesta questão, todos os vetores estão escritos na base canônica). Considere o plano vetorial

E a transformação linear que verifica

E

1. Determine a matriz da transformação linear na base canônica.
2. Determine uma base da imagem de (denotada ). Lembre que
3. Determine uma base do núcleo de (denotado ). Lembre que
4. Determine o conjunto de todos os vetores de que verificam

Sejam o espaço vetorial dos polinômios de grau menor ou igual a dois e o espaço vetorial das matrizes de duas linhas e uma coluna. Considere a transformação dada por

1. Mostre que é uma transformação linear.
2. Determine
3. Encontre, se possível, um polinômio de grau um e tal que . Caso contrário, justifique.
4. Encontre, se possível, um polinômio não nulo pertencente ao núcleo de , ou seja, tal que . Caso contrário, justifique.
5. Determine , ou seja, determine o posto de .

Dentre as transformações lineares abaixo, assinale aquela cujo núcleo é a reta e cuja imagem é a reta

a)

b)

c)

d)

Sabemos que, na transformação linear , o núcleo é a reta e a imagem é a reta Qual das transformações poderia ser

(a)

(b)

(c)

(d)

Sejam A e B matrizes 3x5 com B escalonada. Suponha que B tenha sido obtida a partir de A por aplicação de operações elementares nas linhas. Assinale a alternativa FALSA.

(a) O núcleo de B é igual ao núcleo de A.

(b) As colunas dos pivôs de B formam uma base da imagem de B.

(c) As linhas de B geram o espaço-linha de A.

(d) As colunas de B geram a imagem de A.

Se é o espaço vetorial das matrizes , definimos através de onde e . Então podemos afirmar que a dimensão da imagem de é:

Assinale a transformação linear abaixo, , cujo núcleo é a reta e cuja imagem é a reta

Exiba um operador linear tal que

Decida se cada afirmação abaixo é verdadeira ou falsa. Se a afirmação for verdadeira, apresente uma demonstração. Se a afirmativa for falsa, exiba explicitamente um contraexemplo.

c) Seja o espaço vetorial das matrizes . Se é a transformação linear definida por Onde é uma matriz fixa, então tem posto .

Quais são todos os valores de para os quais a transformação linear dada por é invertível?

qualquer

Decida se cada afirmação abaixo é verdadeira ou falsa. Se a afirmação for verdadeira, apresente uma demonstração. Se a afirmativa for falsa, exiba explicitamente um contraexemplo.

1. Se é uma transformação linear, então a imagem de é um espaço vetorial.

Decida se cada afirmação abaixo é verdadeira ou falsa. Se a afirmação for verdadeira, apresente uma demonstração. Se a afirmativa for falsa, exiba explicitamente um contraexemplo.

1. Se é uma transformação linear, então o núcleo de é um espaço vetorial.

Seja uma transformação linear entre o espaço vetorial dos polinômios de grau até com coeficientes reais, e o espaço vetorial das matrizes coluna com linhas, com elementos reais. Se a matriz associada a , em relação às bases canônicas de e é:

Determine uma base para , o subespaço de cujos elementos são imagem de , para algum .

Determine uma base para , o subespaço de cujos elementos tem imagem .

Dica: A base canônica de é , e seus vetores são escritos, nesta base, simplesmente como ,

Seja o espaço vetorial das matrizes quadradas de duas linhas e duas colunas.

Considere a aplicaçãodada por

b) Determine uma base de Nuc(T) (Núcleo de T).

Considere a transformação linear dada pela matriz

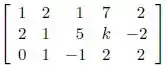
Onde k é uma constante real. Determine, se possível, o que é pedido abaixo em cada item.

Caso não seja possível, justifique.

(a) Todos os valores de k tais que

(b) Todos os valores de k tais que

(c) Todos os valores de k tais que

(d) Todos os valores de k tais que

Lembre que a imagem de uma transformação linear é definida como

a) Considere a transformação linear cuja matriz na base canônica é

Sabendo que o espaço imagem de é uma reta, determine os valores de e .

Dentre as transformações lineares abaixo, assinale aquela cujo núcleo é a reta e cuja imagem é a reta .

Seja uma transformação linear, , cuja imagem é a reta e núcleo é o plano de equação . Assinale uma matriz que representa esta transformação linear:

(a) (b) (c) (d) (e) Não sei

Considere dois vetores não nulos de representados pelas matrizes-coluna u e v, e seja .

I –

II –

(a) I é falsa e II é falsa.

(b) I é falsa e II é verdadeira.

(c) I é verdadeira e II é falsa.

(d) I é verdadeira e II é verdadeira.

14) Sejam um espaço vetorial não nulo de dimensão finita e uma transformação linear tal que . Assinale a alternativa correta:

a) Vale necessariamente que e

b) vale necessariamente que ;

c) vale necessariamente que

d) é possível que ;

e) vale necessariamente que

12) Seja uma transformação linear tal que:

e .

Sabe-se que:

Se e forem tais que , então será igual a:

a)

b)

c)

d)

e)

Seja

A dimensão da imagem de é:

1. 1
2. 4
3. 2
4. 3

Considere uma transformação linear . A dimensão do núcleo de não pode ser:

1. 34
2. 13
3. 40
4. 16

é tal que . Se , calcule a matriz. Assinale abaixo o valor da entrada :

(a)

(b)

(c)

(d)

Seja

Se pertence ao núcleo de , então vale:

1. -5
2. -8
3. -7
4. -6