Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 80b
O paralelogramo tem os lados e paralelos ao eixo transverso da hipérbole e os lados e contidos em retas tangentes a . Os pontos de tangência têm coordenadas inteiras, e um dos lados tem comprimento . Conhecendo , determine e .
Resolva o item , com ‘’eixo conjugado’’ em lugar de ‘’eixo transverso’’
Passo 1
Sabendo que o eixo conjugado é o eixo perpendicular do transversal então temos que as retas e estão na direção do eixo .
As retas tangentes terão o mesmo sentido da letra anterior , já que uma dessas retas tem o ponto .
Aplicando o ponto nessa equação teremos:
Onde é o ponto de tangência.
E aplicando na hipérbole nós teremos:
Então:
Isso nos dará resultados para iguais a e , porém como nos diz que os pontos de tangência são números inteiros então , e será
Isso nos dará uma equação de reta tangente igual a:
Ou
E a outra reta tangente será como vimos na letra anterior.
Passo 2
E como o vértice desse paralelogramo está a de distância do ponto e pertence a mesma reta então:
Raízes iguais a e .
Teremos duas posições possíveis para , uma em e e outra em e .
Passo 3
Como sabemos a equação da outra reta tangente isso nos permite matar os pontos que estão em retas paralelas ao eixo conjugado como e , pois eles estão a dois de distância de e respectivamente (a reta está a duas casas para baixo de , aplique e veja a distância em das duas retas). Então:
Os ponto e estão em , portanto soma-se 2 em y para encontrar suas coordenadas. Para cumprir o paralelismo com o eixo conjugado.
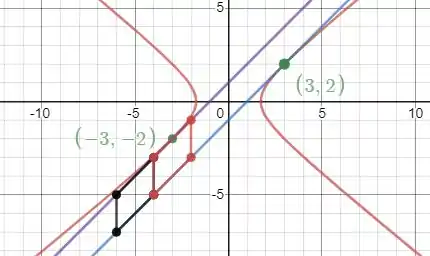
Um gráfico dessa questão pode ser visto abaixo.
Resposta
Ou