Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 18
Mostre que a amplitude focal da hipérbole é .
Passo 1
Vamos lá! Estamos trabalhando aqui com uma hipérbole. Precisamos provar então uma relação para sua amplitude focal.
Para facilitarmos a nossa vida, vamos assumir que a hipérbole está centrada na origem e com focos no eixo (isto não impacta na nossa análise em problema nenhum).
Portanto, a nossa hipérbole possui a seguinte equação:
E focos nos pontos , onde .
Passo 2
Certo. Utilizamos o passo 1 para definir a nossa hipérbole. Mas não é isto que a questão quer! Ela quer saber o comprimento da amplitude focal! Como proceder em relação a isso?
Antes de tudo. O que é a amplitude focal???
Bom, amplitude focal nada mais é do que uma corda da hipérbole (toca em dois pontos) e que é perpendicular ao segmento focal. Podemos ver abaixo a amplitude focal (segmento em vermelho):
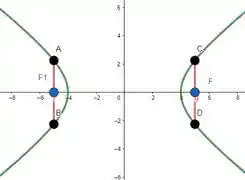
Portanto, nosso trabalho é identificar quais são as coordenadas destes pontos que pertencem a hipérbole e são perpendiculares ao segmento focal e depois calcularmos a distância entre dois pontos!
E bom, podemos fazer isto de uma forma bem simples. Vamos analisar para os pontos e (mesmo procedimento para o ponto e ). Como pode ser observado pela imagem, os pontos e estão bem acima/abaixo do ponto . Portanto, eles possuem a mesma coordenada do foco .
Em outras palavras, podemos escrever as coordenadas do ponto da seguinte forma: . A questão é descobrir quem é este que satisfaça a equação da hipérbole, visto que assumimos que o ponto pertence a hipérbole!
Passo 3
Vamos descobrir agora quem é este das coordenadas de Então, basta substituirmos as coordenadas de na equação da hipérbole! Portanto,
Só que , pela definição da hipérbole. Portanto,
Tirando a raiz, vamos obter:
Cuidado para não se esquecerem do sinal negativo também! Enquanto o positivo será a coordenada do ponto , o valor negativo será o do ponto . Portanto, temos os seguintes pontos:
OBS: Se tivéssemos analisados os pontos e , a única diferença das coordenadas dos pontos seria a coordenada , que teria o valor . O valor de também seria .
Agora, só nos resta calcularmos a distância dos dois pontos para sabermos o comprimento do segmento focal. Portanto,
E assim provamos a relação da questão!