Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 21.Exercício - Ex. 7
Seja o sistema obtido pela translação do sistema ortogonal para um ponto pertencente a reta . Determine, em cada caso, as coordenadas de em relação a .
dista de .
dista de
Passo 1
Essa reta nos diz que:
Ou seja:
Passo 2
E quando dizemos que o ponto dista 3 de , nós queremos dizer que esse ponto dista três do plano no sistema de coordenada com o ponto .
Então para o ponto distar do plano e sabendo que esse ponto está em relação ao sistema de coordenadas de , logo:
Pois a distância ao plano é inteiramente no eixo .
Como pode ser visto na figura abaixo:
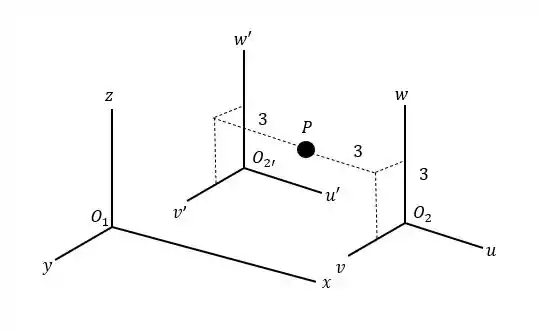
O novo sistema de coordenadas formado por pode estar a esquerda ou a direita do , devemos levar em consideração os dois casos.
Passo 3
Como o ponto pertence a reta , então:
Para :
Então o primeiro ponto (no primeiro sistema de coordenadas) para na letra será:
E para :
E o outro ponto então será:
Passo 4
Agora para o caso da letra teremos a situação inversa:
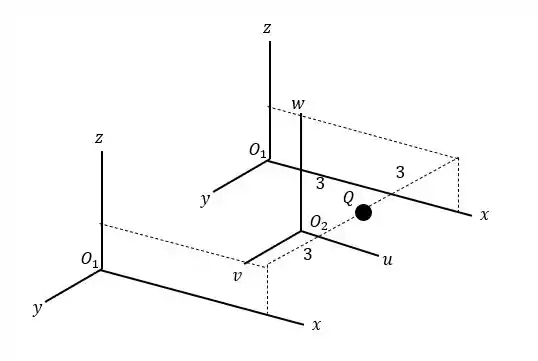
Nesse caso a coordenada pode estar em duas posições diferentes (em relação ao sistema de coordenadas 2), o que afeta diretamente a posição de em relação a (só que não se esqueça que a reta está em relação as coordenadas de ). Isso nos quer dizer que a coordenada de será , e como na coordenada de ela está em , então podemos escrever que a coordenada em de será:
Pois a coordenada dista de do ponto , sempre de forma mais distante a coordenada 1.
Passo 5
Como continua pertencendo a reta , então:
Para :
Logo o primeiro ponto para na coordenada de será:
E para :
E o segundo ponto será: