Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 9.Problemas propostos - Ex. 12

12. Determinar os vértices e os focos da elipse

(x^2)/(2) + (y^2)/(8) - (z^2)/(9) = 1 , z = 3

Passo 1

A primeira coisa que temos que fazer aqui é substituir o valor de z = 3 na equação dada (do hiperboloide):

(x^2)/(2) + (y^2)/(8) - (3^2)/(9) = 1 ->

(x^2)/(2) + (y^2)/(8) - 1 = 1 ->

(x^2)/(2) + (y^2)/(8) = 2

Passando esse 2 do outro lado dividindo...

(x^2)/(4) + (y^2)/(16) = 1

Ou ainda...

(x^2)/(2^2) + (y^2)/(4^2) = 1

Passo 2

Beleza, agora que temos a equação da elipse, vejamos: se trata de uma elipse ao redor da origem, portanto, os vértices da elipse acontecem quando...

x = 0 o u y = 0

Se...

x = 0 -> (0^2)/(2^2) + (y^2)/(4^2) = 1 -> y^2 = 4^2 -> y = +- 4

Se...

y = 0 -> (x^2)/(2^2) + (0^2)/(4^2) = 1 -> x^2 = 2^2 -> x = +- 2

Então, lembrando que estamos falando de uma elipse em cima do plano z = 3 , para o primeiro caso ( x = 0 ) teremos dois vértices:

x = 0 -> d o i s v é r t i c e s : (0 , 4 , 3) e (0 , - 4 , 3)

Para o segundo caso...

y = 0 -> d o i s v é r t i c e s : (2 , 0 , 3) e (- 2 , 0 , 3)

Agora falta descobrir os focos!

Passo 3

Poxa! Sabemos que o foco da elipse é de tal maneira que...

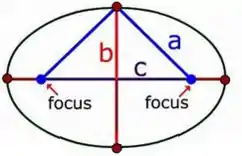
Onde a é o valor maior abaixo ou de x ou de y ( b o menor):

(x^2)/(2^2) + (y^2)/(underset(a = 4)(ubrace 4^2)) = 1

Então, se a = 4 e b = 2 , c (o foco) vai ser...

c^2 = a^2 - b^2 ->

c = +- sqrt(4^2 - 2^2) ->

c = +- 2 sqrt(3)

Reparando que o foco acontece sempre no maior eixo (eixo onde está a ), então podemos falar que no nosso caso, o foco acontece em cima do eixo y . Então, os pontos de foco serão:

(0 , +- 2 sqrt(3) , 3)

Resposta

Vértices: (0 , +- 4 , 3) e (+- 2 , 0 , 3)

Foco: (0 , +- 2 sqrt(3) , 3)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Identificar e representar graficamente as superfícies expressas pelas equações nos intervalos dados.j) z = 4 - 2 x 2 - y 2 , 0 ≤ z ≤ 4
Identificar e representar graficamente as superfícies expressas pelas equações nos intervalos dados.i) x = - 4 + y 2 1 + z 2 ,- 4 ≤ x ≤ 5
7. Identificar as superfícies definidas pelas equações, dizendo ao longo de que eixo elas ocorrem, conforme o caso. a )25 x 2 + 100 y 2 + 36 z 2 - 900 = 0
7. Identificar as superfícies definidas pelas equações, dizendo ao longo de que eixo elas ocorrem, conforme o caso. h )z = 4 + 4 x 2 + 4 y 2
7. Identificar as superfícies definidas pelas equações, dizendo ao longo de que eixo elas ocorrem, conforme o caso. g )z = x 2 + y 2 - 1