Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 9.Problemas propostos - Ex. 6l

6. Identificar e representar graficamente as superfícies expressas pelas equações nos intervalos dados.

l )   y 2 + 4 z 2 - 4 = 0 ,   - 4 ≤ x ≤ 6

Passo 1

L e t r a   l :

Fala aí! Nesse exercício daqui estaremos trabalhando a seguinte equação:

y 2 + 4 z 2 - 4 = 0

POXA! O primo dessa equação, y 2 + 4 z 2 = 4

Não é uma elipse no plano y z ? Então, a ausência do x , indica que ao em 3 D , essa equação representará um CILÍNDRO ao redor do eixo x , como vimos na teoria. Além disso, a sua diretriz é elíptica:

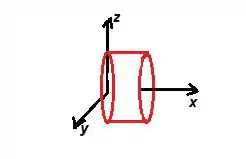
OBSERVAÇÃO: Essa ainda não é a representação gráfica da nossa equação e sim apenas um esboço de quem ela vai ser ok? Se quiser ver como se desenha perfeitamente essa quádrica, venha comigo para o próximo passo!

Passo 2

  1. Primeiro repare que só queremos a parte que vai de x = - 4 até x = 6 , já o exercício nos impôs a condição de que - 4 ≤ x ≤ 6 .
  2. Segundo, repare bem que a diretriz (ou a “base”) é uma elipse de eixo maior em y :

y 2 + 4 z 2 = 4     →

y 2 4 + z 2 = 1   →

y 2 2 2 + z 2 1 2 = 1  

Com essas informações, e tendo em mente o nosso esboço do passo 1, podemos finalmente desenhar a nossa quádrica:

Viu só!

Resposta

Cilindro ao redor do eixo x e de diretriz elíptica.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a equação da superfície de revolução gerada pela rotação da curva dada em torno do eixo especificado. a) 9 x 2 + 4 y 2 = 36ez = 0 em torno do eixo y.
Demonstre que existe apenas um plano tangente à superfície esférica x 2 + y 2 + z 2 - 2 x + 6 y + 2 z + 8 = 0 que contém a reta x = 4 t + 4 , y = 3 t + 1 , z = t + 1 . Escreva sua equação.
Mostre que a interseção de um cone circular com plano que não passa pelo seu vértice e uma cônica seguindo os seguintes passos:a) considere dois sistemas de coordenadas R = O , i → , j → , k →e S = O
Determine a interseção da esfera x ² + y ² + z ² =8 ² ² ² com o conjunto C={ ( x ,y ,z )∈R ³;z= x 2 + y ²} ³ ² . Esboce geometricamente a situação
Complete os quadrados e decida para quais valores de k a equação x ²+y ²+z ²+x+2 y+3 z+k =0 ² ² ² define um ponto, uma esfera ou o conjunto vazio?