Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 2.Problemas Propostos - Ex. 30
Se , e o ângulo entre os vetores e , determinar o ângulo entre e e construir uma figura correspondente a esses dados.
Passo 1
Então galera, antes de qualquer coisa vamos esboçar esses dois vetores, assim como o ângulo formado entre eles, se liga:
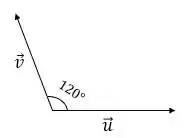
Show! Queremos encontrar o ângulo entre e , certo? Geometricamente, essas duas somas ficaria assim:
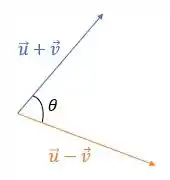
Então o que queremos encontrar é esse bendito ângulo aí! Bora que bora!
Passo 2
de acordo com o que estudamos no capítulo em questão do Winterle, temos que o produto escalar entre dois vetores é dado da seguinte forma:
No qual é o ângulo entre os dois vetores. No nosso caso, nossos vetores são e , logo:
Para o numerador, teremos:
Como e , então:
Ok, a primeira parte foi feita!
Passo 3
Agora para o denominador temos que calcular dois módulos, certo? O primeiro é , então:
Substituindo os valores:
Analogamente, para teremos:
Substituindo os valores:
Voltando para a expressão do ângulo entre os vetores, teremos: