Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 2.Problemas Propostos - Ex. 31d
31. Seja o cubo de aresta representado na Figura 2.17.
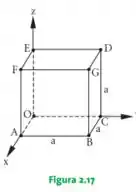
Determinar:
d)
Passo 1
Então galera, o enunciado quer que determinemos os módulos dos vetores e , certo? Se traçarmos quem são esses vetores no desenho, teremos:
Note que não estamos interessados no ângulo formado entre os vetores, nem nada do tipo. Estamos tratando dos vetores separadamente, tudo bem? Show! Para determinarmos o módulo de um vetor temos que saber quanto vale suas componentes, e de acordo com a figura temos o seguinte, pessoal:
Agora que temos as componentes dos vetores, basta utilizarmos o Teorema de Pitágoras para ambos vetores. Bora que bora!
Passo 2
Para o primeiro vetor, teremos:
Por fim, para o segundo e último vetor, teremos:
E esses são os módulos dos vetores, galera! 😊
Resposta
Exercícios de Livros Relacionados
Se um vetor tem ângulos diretores α = π 4 e β = π 3 , determine o terceiro ângulo diretor γ .
Prove que u ∙ v =± u v se, e somente se, um dos vetores u, v é múltiplo do outro. Em seguida, compare u + v 2 = ( u + v∙ u + v ) com u + v 2 para concluir que u + v = u + | v | se, e somente se, um do
Dados u → = - x - 1,2 , 1 , v → = - 3 , x , 1ew → = x - 4,0 , 1 , determine x para que os vetores u → ,v →ew → sejam coplanares e dois a dois não paralelos. Para esse valor de x , escreva w → como com
Sabendo que os vetores a → , b →ec → são l . i . , determine o menor m tal que u → = a → + b → + c → , v → = 4 a → + m b → + c → e w → = b → + m c → sejam l . d . Com esse m , escreva t → = a → - b →
Sejam u → = m , - 1 , m 2 + 1 , v → = ( m 2 + 1 , m , 0 ) e w → = m , 1,1 . Mostre que C = ( u → , v → , w → ) é uma base de V , independentemente do valor de m .