Enunciado
Álgebra Linear e Geometria Analítica - Reginaldo - Matrizes, Vetores e Geometria Analítica- Ed: 1º - Capítulo 6.1 - Ex. 1.b
6.1.1. Reduzir cada uma das equações de forma a identificar a quádrica que ela representa e faça um esboço do seu gráfico:
(b) x2+y2+z2 = 0
Passo 1
O primeiro passo é sem dúvidas alguma, expandir a equação, de forma a encontrar a quádrica a qual ela pertence, sendo assim, pode constatar que a equação da questão é equivalente à:
Passo 2
O segundo passo é encontrar a quádrica a qual essa equação pertence, e para isso, basta compará-la as equações gerais das quádricas. Nesse sentido, pode-se inferir que esta equação representa um PARABOLÓIDE ELIPTICO que pode ser descrito pela seguinte equação geral:
Passo 3
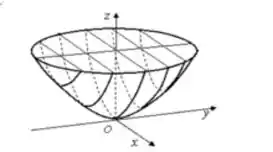O terceiro e último passo é esboçar o gráfico do paraboloide elíptico, que deve seguir o molde dessa imagem, ajustando-se a cada equação.
Resposta
PARABOLÓIDE ELÍPTICO
Exercícios de Livros Relacionados
7. Identificar as superfícies definidas pelas equações, dizendo ao longo de que eixo elas ocorrem, conforme o caso. f )12 x 2 + 4 y 2 - 3 z 2 + 12 = 0
8. Identificar a superfície S e a sua interseção com o plano π dado. Representar graficamente esta interseção no plano π . c )S : z = - x 2 4 + y 2 9eπ : z = 1
8. Identificar a superfície S e a sua interseção com o plano π dado. Representar graficamente esta interseção no plano π . a )S : y 2 - 4 z 2 - 2 x = 0eπ : x - 2 = 0
12. Determinar os vértices e os focos da elipse x 2 2 + y 2 8 - z 2 9 = 1 , z = 3
6.1. 4. Determine a equação do lugar geométrico dos pontos P (x, y, z) tais que a soma das distâncias de P aos dois pontos (2, 0, 0) e (−2, 0, 0) é igual a 6. Que lugar geométrico é este?