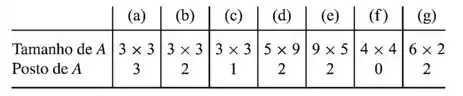
Em cada parte, use a informação na tabela para encontrar as dimensões do espaço linha de , do espaço coluna de , do espaço nulo de e do espaço nulo de .
Passo 1
Olá! Tudo bem? Para resolver esse exercício precisaremos saber que:
1. O posto de uma matriz é definido como a dimensão do espaço linha e, também, do espaço coluna, veja:
2. Uma matriz de tamanho , com , possui nulidade igual a :
3. Quando temos uma matriz transposta, seu posto não muda, mas seu tamanho sim. Portanto, se tem tamanho , tem tamanho e a nulidade de é:
Passo 2
Com base no que foi dito no Passo 1 podemos responder nosso exercício, o qual foi posto em forma de tabela, para simplificar. Veja:
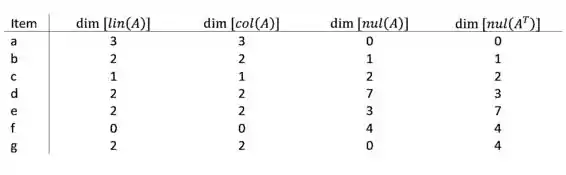
Resposta
Ver Passo 2.