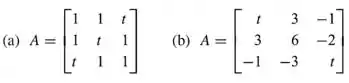
Em cada parte, discuta como o posto de varia com .
Passo 1
Olá! Tudo bem? Vamos resolver esse exercício?!
(a) Primeiro, se tentarmos reduzir para sua forma escalonada, descobrimos que:
se
se
se
Portanto, se . Se , pelo cálculo direto. Se , . Se , .
Resposta
Veja a resolução completa.