Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 8.Hipérbole - Ex. 37

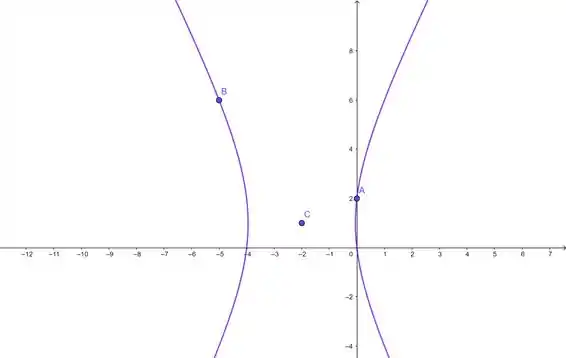
Em cada um dos problemas de 14 a 37, determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.

Centro C ( - 2,1 ) , eixo real paralelo a O x e passando por ( 0,2 ) e ( - 5,6 ) .

Passo 1

Opaaa! Tudo joia?

O problema nos deu o centro, dois pontos pertencentes à hipérbole e que o eixo é paralelo a O x .

Vamos pensar em como usar isso...

Olha os pontos:

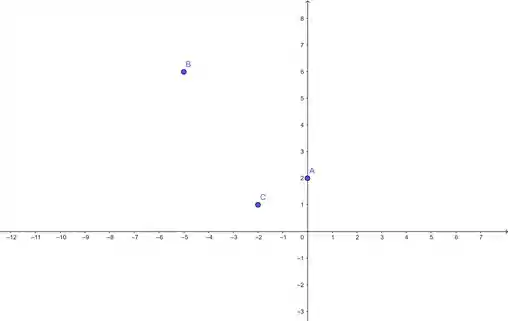
O C é o centro e os outros dois pontos pertencem à hipérbole.

Complicou né? Mas calma... vem comigo!

Passo 2

Como o eixo é paralelo ao eixo x , a equação é da forma:

x - h 2 a 2 - y - k 2 b 2 = 1

Usando o centro que o problema nos deu, ficamos com:

x + 2 2 a 2 - y - 1 2 b 2 = 1

A gente tem que achar esses a   e   b aí...

Pra isso, vamos usar os pontos que pertencem à hipérbole!

Passo 3

Substituindo os pontos 0,2     e   ( - 5,6 ) na equação do passo 2, a gente vai ter:

0 + 2 2 a 2 - 2 - 1 2 b 2 = 1

4 a 2 - 1 b 2 = 1

4 b 2 - a 2 a 2 b 2 = 1

4 b 2 - a 2 = a 2 b 2   ( * )

o outro ponto...

- 5 + 2 2 a 2 - 6 - 1 2 b 2 = 1

9 a 2 - 25 b 2 = 1

9 b 2 - 25 a 2 a 2 b 2 = 1

9 b 2 - 25 a 2 = a 2 b 2     ( * * )

Juntando ( * ) e ( * * ) , temos:

4 b 2 - a 2 = 9 b 2 - 25 a 2

Vish.... e agora?

Passo 4

Parece que não vai dar em nada ali né? Mas calma lá! Vamos colocar o b em função de a ...

- 5 b 2 = - 24 a 2

b 2 = 24 5 a 2   ( * * * )

Com essa relação, a gente pode substituir em ( * ) :

4 24 5 a 2 - a 2 = a 2 24 5 a 2

96 5 a 2 - a 2 = 24 a 4 5

96 a 2 - 5 a 2 = 24 a 4

91 a 2 = 24 a 4

24 a 2 = 91

a 2 = 91 24

Show! Voltando esse valor em ( * * * ) achamos b 2 :

b 2 = 24 5 91 24

b 2 = 91 5

Ufaaa! Encontramos os termos da nossa equação! Ela é:

x + 2 2 91 / 24 - y - 1 2 91 / 5 = 1

Passo 5

A gente não pode deixar dessa forma de equação reduzida aqui, então vamos desenvolver pra achar a equação geral:

24 x + 2 2 91 - 5 y - 1 2 91 = 1

24 x + 2 2 - 5 y - 1 2 = 91

24 x 2 + 4 x + 4 - 5 y 2 - 2 y + 1 = 91

24 x 2 + 96 x + 96 - 5 y 2 + 10 y - 5 = 91

24 x 2 - 5 y 2 + 96 x + 10 y = 0

Prontinho! Finalmente chegamos à bendita da equação da hipérbole!

Passo 6

E por último, mas não menos importante, o esboço do gráfico da hipérbole:

Resposta

24 x 2 - 5 y 2 + 96 x + 10 y = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Obtenha, em cada caso, uma equação reduzida da hipérbole:Os vértices são 2,0 e - 2,0 e os focos, 3,0 e - 3,0 .Os vértices são - 15,0 e 15,0 e as assíntotas tem equações 5 y - 4 x = 0 e 5 y + 4 x = 0 .
A hipérbole H tem centro O, focos em um dos eixos coordenados, e contém os pontos A e B. Escreva equações reduzidas de H e de suas assíntotas e determine os focos e vértices. A = 6 , 7 , B = - 1,0 . A
Obtenha, em cada caso, uma equação reduzida da hipérbole:Os vértices são 2,0 e - 2,0 e os focos, 3,0 e - 3,0 .Os vértices são - 15,0 e 15,0 e as assíntotas tem equações 5 y - 4 x = 0 e 5 y + 4 x = 0 .
Obtenha, em cada caso, uma equação reduzida da hipérbole:Os vértices são 2,0 e - 2,0 e os focos, 3,0 e - 3,0 .Os vértices são - 15,0 e 15,0 e as assíntotas tem equações 5 y - 4 x = 0 e 5 y + 4 x = 0 .
Obtenha, em cada caso, uma equação reduzida da hipérbole:Os vértices são 2,0 e - 2,0 e os focos, 3,0 e - 3,0 .Os vértices são - 15,0 e 15,0 e as assíntotas tem equações 5 y - 4 x = 0 e 5 y + 4 x = 0 .