Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 8.Elipse - Ex. 22
Em cada um dos Problemas de 20 a 27, obter uma equação da elipse que satisfaça as condições dadas.
Focos e e excentricidade
Passo 1
O enunciado nos da os dois focos, e o centro esta exatamente no meio entre eles, então vamos fazer
Beleza, agora que temos o centro e o foco, a distancia focal vai ser a distancia do do centro até o de um dos focos, então temos que:
Agora para achar , vamos usar a relação
Passo 2
Agora para acharmos , vamos fazer aquela relação do triangulo da elipse, se você não lembra é essa relação aqui da imagem:
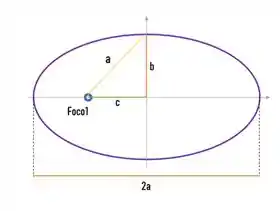
No caso dessa questão, nossa elipse é “em pé” porque a distancia focal está em y
Passo 3
Agora vamos montar a nossa equação da elipse, lembrando que como o centro não está na origem, e a distancia focal está relacionada ao eixo y, ficamos com essa equação:
Subsituindo os valores que temos de e e de e (são as coordenadas do centro) ficamos com:
Podemos ajeitar isso ai e ficamos com