Para cada uma das regiões do plano descritas a seguir, escreva uma desigualdade ou sistema de desigualdades que a defina:

b) A região formada pelo interior e os lados do triângulo cujos vértices são (0, 0), (3, 3) e (4, 0).

Salve galera estudiosa, tudo certin?? É hora da resolução!!! Vamos lá??

Primeiramente, nos foi dado um conjunto de vértices que formam a nossa região, para melhorar a compreensão, vamos visualizar esses pontos no plano cartesiano.

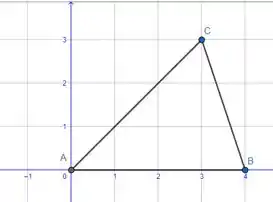
Precisamos usar nossos conhecimentos para determinar as retas que delimitam esse triângulo.

A reta que passa pelos pontos A e B é bem conhecida. É o próprio eixo X, que é definida pela equação y = 0.

A nossa região está representada acima da reta y = 0, logo temos a nossa primeira desigualdade:

A reta que passa pelos pontos A e C também é bem conhecida. É a bissetriz entre o primeiro e terceiro quadrante, dada pela equação y = x ou ainda x – y = 0.

A nossa região está representada abaixo da reta x – y = 0, logo temos a nossa segunda desigualdade:

Note que a reta que passa pelos pontos B e C pode ser determinada através de um sistema de equações do primeiro grau. O que nos daria a equação y = -3x + 12 ou ainda 3x + y = 12.

A nossa região está representada abaixo da reta 3x + y = 12, logo temos a nossa segunda desigualdade:

Logo, nosso semi-plano é determinado pelo conjunto das desigualdades encontradas, ou seja:

Visualmente, teríamos a região representada no gráfico a seguir: