Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 7.Exercícios Propostos - Ex. 2

Determine k de modo que o ponto ( 3,1 , k ) pertença ao plano determinado por A   =   ( 1,1 , 2 ) , B   =   ( 3,0 , 2 ) e C   =   ( 4,1 , 3 ) .

Passo 1

Galera, o raciocínio aqui é o seguinte: primeiro encontramos o plano determinados pelos pontos A   =   ( 1,1 , 2 ) , B   =   ( 3,0 , 2 ) e C   =   ( 4,1 , 3 ) e depois substituímos ( 3,1 , k ) na equação do plano para determinar k . Vamos lá!

Os pontos fornecidos pela questão nos dão os seguintes vetores:

A B → = B - A = ( 3,0 , 2 ) -   ( 1,1 , 2 ) = ( 2 , - 1,0 )

A C → = C - A = ( 4,1 , 3 ) -   ( 1,1 , 2 ) = ( 3,0 , 1 )

Passo 2

Agora, escolhemos um ponto X = ( x , y , z ) presente no plano, de modo que

A X → = X - A = ( x , y , z ) - ( 1,1 , 2 ) = ( x - 1 , y - 1 , z - 2 )

Como os vetores A X → , A B → e A C → são l.d., o seguinte determinante deve ser nulo:

⇒ - ( x - 1 ) - 2 ( y - 1 ) + 3 ( z - 2 ) ⇒ - x + 1 - 2 y + 2 + 3 z - 6 = 0

⇒ - x - 2 y + 3 z - 3 = 0 ⇒ x + 2 y - 3 z + 3 = 0

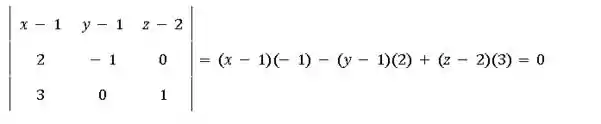
Passo 3

Prontinho, já temos a equação do plano. Agora, vamos substituir ( 3,1 , k ) nessa equação para determinar k

x + 2 y - 3 z + 3 = 0 ⇒ 3 + 2 - 3 k + 3 = 0 ⇒ - 3 k + 8 = 0 ⇒ k = 8 3

Resposta

k = 8 3

Exercícios de Livros Relacionados

Sejam AB e CD retas paralelas. Ache uma equação para o plano determinado por elas.
Dados os pontos A=( 1 ,1 ,2 ) ,B=( 1 ,2 ,3 )eC=( - 1 ,2 ,1 ) , obtenha as coordenadas de um ponto P tal que o segmento O P seja perpendicular ao plano A B C . Use as coordenadas de P para achar uma eq
Obtenha uma equação para o plano que contém o ponto P e é perpendicular ao segmento de reta A B nos seguintes casos: a )P=( 0 ,0 ,0 ) ,A=( 1 ,2 ,3 ) ,B=( 2 ,- 1 ,2 ) ; b )P=( 1 ,1 ,- 1 ) ,A=( 3 ,5 ,2
Qual é o simétrico do ponto P=( 3 ,7 ,0 ) em relação ao plano x+2 y-z=5 ?
Existe um plano que passa pela origem e contém o ponto P=( x + 2 y + 3 z ,- 2 x +y-z ,- x+8 y+7 z ) , sejam quais forem os valores atribuídos a x ,yez . Ache a equação desse plano.