Enunciado

Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 11.Problemas - Ex. 2c

Para cada uma das regiões do plano descritas a seguir, escreva uma desigualdade ou sistema de desigualdades que a defina:

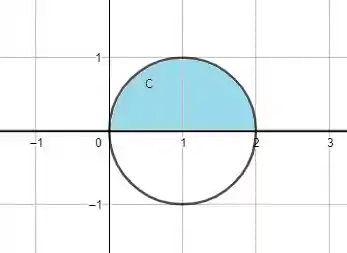
c) A parte da circunferência de centro (1, 0) e raio 1 situada acima do eixo OY.

Passo 1

Salve galera estudiosa, tudo certin?? É hora da resolução!!! Vamos lá??

Primeiramente, vamos visualizar melhor essa circunferência, desenhando o seu gráfico, obtemos:

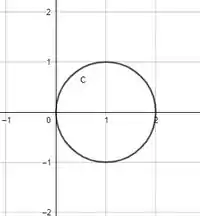
Temos que a equação dessa circunferência é dada por:

Para delimitar a região que seria interior à circunferência, temos a seguinte desigualdade:

O eixo OY é o próprio eixo X, que é definida pela equação y = 0.

A nossa região está representada acima do eixo, logo temos a nossa segunda desigualdade:

Logo, o conjunto de desigualdades que define a região do semi-plano é dado por:

Que poder representada visualmente pelo gráfico a seguir:

Resposta

Exercícios de Livros Relacionados

Uma mudança de eixos no plano manteve a origem fixa, enquanto as coordenadas dos pontos 1 ,0 e0 ,1 passaram a ser a ,b ec ,d respectivamente. Quais são as novas coordenadas do ponto 2 ,3 ?

Uma mudança de coordenadas passou do sistema O X Y para O' X'Y' . O ponto ( 3 ,1 ) é a nova origem e os pontos ( 5 ,2 ) e ( 2 ,3 ) pertencem aos semi-eixos positivos O' X' e O'Y' respectivamente. Quai

Um subconjuntoC do plano chama-se convexo quando o segmento de reta que une dois pontos quaisquer de C está contido em C . Prove que o conjunto das soluções de um sistema de desigualdades lineares a d

Resolva o exercício anterior escrevendo, por meio de equações, a condição para que cada um dos pontos A ,BeC pertença ao plano a x+b y+c z=d .

Supondo a b c≠0 , escreva a equação do plano que corta os eixos O X ,O YeO Z nos pontos ( a ,0 ,0 ) ,( 0 ,b ,0 )e( 0 ,0 ,c ) respectivamente.