Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 44

Calcule, em cada caso, a excentricidade da hipérbole H .

  1. 4 x 2 - y 2 = 16 .
  2. x 2 - 2 y 2 + 8 = 0 .
  3. O triângulo F 1 B 2 F 2 é retângulo.
  4. As diagonais do retângulo fundamental formam ângulos de 60 ° .
  5. Os pontos A 1 ,   A 2 ,   B 1 e B 2 são vértices de um quadrado.

Passo 1

  1. Podemos escrever

    2. 4 x 2 - y 2 = 16 ⟺

    4 x 2 16 - y 2 16 = 1 ⟺

    x 2 4 - y 2 16 = 1

    Assim, vemos que a 2 = 4 e b 2 = 16 . Assim,

    c 2 = a 2 + b 2 = 4 + 16 = 20 ∴ c = 2 5

    Portanto,

    e = c a = 2 5 2 = 5

    Passo 2

  2. Podemos escrever

    3. x 2 - 2 y 2 + 8 = 0 ⟺

    2 y 2 - x 2 = 8 ⟺

    y 2 4 - x 2 8 = 1

    Assim, vemos que a 2 = 4 e b 2 = 8 . Assim,

    c 2 = a 2 + b 2 = 4 + 8 = 12 ∴ c = 2 3

    Portanto,

    e = c a = 2 3 2 = 3

    Passo 3

  3. Veja a figura abaixo

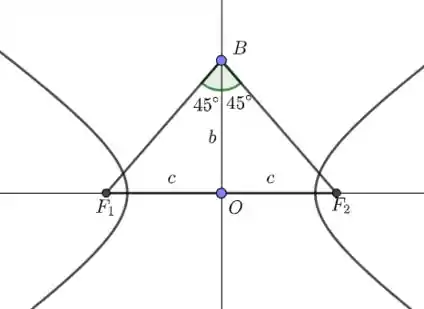
    4. Note que teríamos o triângulo B F 1 O , retângulo em O , e isósceles, de modo que

    b = c

    Porém, sabemos que em uma hipérbole

    c 2 = b 2 + a 2

    o que mostra que c > b e c > a . Portanto, tal hipérbole não existe!

    Passo 4

  4. Podemos ter

    5. b a = tan ⁡ 60 ° ⟹ b = 3 a

    c 2 = a 2 + b 2 ∴ c 2 = a 2 + 3 a 2 = 4 a 2 ⟹ c = 2 a

    ∴ e = c a = 2 a a = 2

    Ou então,

    a b = tan ⁡ 60 ° ⟹ b = a 3

    c 2 = a 2 + b 2 ∴ c 2 = a 2 + a 2 3 = 4 a 2 3 ⟹ c = 2 3 a 3

    ∴ e = c a = 2 3 a / 3 a = 2 3 3

    Passo 5

  5. Se A 1 ,   A 2 ,   B 1 e B 2 são vértices de um quadrado, então a = b .

Dessa forma,

c 2 = a 2 + b 2 = a 2 + a 2 = 2 a 2 ⟹ c = 2 a

e = c a = 2 a a ⟹ e = 2

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas de 1 a 12 , esboçar o gráfico e determinar os vértices, os focos, a excentricidade e as equações das assíntotas das hipérboles dadas.3. 16 x 2 - 25 y 2 - 400 = 0
Em cada um dos problemas de 1 a 12 , esboçar o gráfico e determinar os vértices, os focos, a excentricidade e as equações das assíntotas das hipérboles dadas.9. y 2 - x 2 = 2
13. Esboçar o gráfico de uma hipérbole (com suas assíntotas) de centro 0 ,0 , eixo real sobre O x e excentricidade:a) 5 3
Usando coordenadas polares r ,θ no plano ( x = r cos ⁡ θ ,y = rs e nθ ) e a definição de cônica dada por 11.7.4, parte 3, você pode deduzir de modo simples as equações polares das cônicas, tomando o p
5.1.3. Escreva as equações das seguintes hipérboles: (b) Os focos são F1 = (−1, −1) e F2 = (1, 1) e satisfaz | distância (P, F1) – distância (P, F2)| = 2;