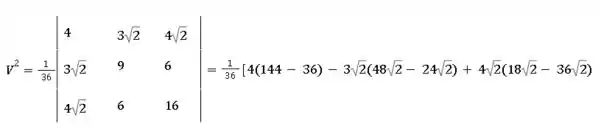Enunciado
Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 5.Exercícios Propostos - Ex. 9
Calcule o volume do tetraedro , sabendo que , e medem, respectivamente, 2, 3, 4, que (veja o exercício resolvido 4 e calcule um produto misto elevado ao quadrado).
Passo 1
Vamos seguir a sugestão do livro e calcular o seguinte produto misto elevado ao quadrado:
onde usamos a relação . Agora, vamos calcular cada um desses produtos internos, sabendo que , e medem, respectivamente, 2, 3, 4 e que :
Passo 2
Vamos pegar todos os produtos internos calculados no passo anterior e substituir no produto misto ao quadrado:
Resposta
Exercícios de Livros Relacionados
4. Sabendo que (u , w , x) = 2 e (v , w , x) = 5 , calculara) (u , x , - w) b) (3 u , 3 w , - 2 x) c) (2 u + 4 v , w , x) d) (5 u - 3 v , 2 w , x)
Verificar se são coplanares os vetores:b) vec u = (2 , - 1,3) , vec v (3,1 , - 2) e vec w = ( 7 , - 1,4 )
Verificar se são coplanares os pontos:A (1,1 , 0) , B (- 2,1 , - 6) , C (- 1,2 , - 1) e D ( 2 , - 1 , - 4 )
Calcular o valor de m para que o volume do paralelepípedo determinado pelos vetores v 1 → = 0 , - 1,2 ,v 2 → = - 4,2 , - 1e v 3 → = ( 3 , m , - 2 ) seja igual a 33 . Calcular a altura desse paralelepí
Determinar o valor de k para que sejam coplanares os vetores: u → = 2 , - 1 , k ,v → = 1,0 , 2 e w → ( k , 3 , k )