1. Construa uma base ortonormal positiva tal que seja paralelo a e coplanar com e .
2. Sendo e , calcule: as coordenadas de na base , e na base .

1. Fala, galera! Mais uma questão para a gente detonar! Então vamos lá! Para que seja paralelo a , devemos ter

Como a base deve ser ortonormal, então todos os vetores devem ter módulo igual a 1. Assim,

O fato de ser coplanar com e indica que os três vetores pertencem ao mesmo plano. Então pode ser escrito como combinação linear de e :

Já o vetor será da forma . Como a base é ortonormal positiva, o produto vetorial do primeiro vetor com o segundo deve gerar o terceiro, do segundo com o terceiro deve gerar o primeiro e do terceiro com o primeiro deve gerar o segundo. Vamos calcular cada um desses produtos vetoriais e ver que conclusões podemos tirar:

• Do primeiro vetor com o segundo:

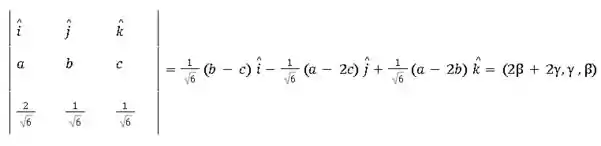
Vamos multiplicar a segunda e terceira equações por 2:

Somando a segunda e terceira equações, obtemos

Agora, comparando o resultado acima com a primeira equação, vemos que

Substituindo esse resultado na primeira equação, obtemos

Vamos resumir os resultados que temos até agora:

Agora ficou fácil de determinar usando a condição de ortonormalidade, isto é, do módulo ser igual a 1:

Podemos também substituir em

Agora, e, utilizando a condição de ortonormalidade, obtemos:

Elevando ambos os lados ao quadrado, obtemos:

Assim, ficamos com

Assim, ficamos com