Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 5.Exercícios Propostos - Ex. 7

Dados O A →   =   ( 2 , - 1,0 ) , O B →   =   ( 1 , - 2,1 ) e O C →   =   ( 1,0 , 2 ) , determine um vetor O D →   =   ( x , y , z ) tal que O D → ,   O A → ∧ O B → , O A → ∧ O C → sejam l.d., O D → ⋅ O B → = - 28 e o volume do tetraedro OABC seja 14.

Passo 1

Para determinar O D →   =   ( x , y , z ) , temos uma série de informações. A primeira que podemos usar é que

O D → ⋅ O B → = - 28 ⇒ ( x , y , z ) ⋅ ( 1 , - 2,1 ) = - 28

⇒ x - 2 y + z = - 28

Também sabemos que o volume do tetraedro é 14. Como o volume é dado pela expressão

V = 1 6 | [ O A , → O B → , O D → ] |

e o produto misto é dado por

[ O A , → O B → , O D → ] = - 4 z - 2 y + z - x = - x - 2 y - 3 z

então,

V = 1 6 | [ O A , → O B → , O D → ] | = 1 6 | - x - 2 y - 3 z | = 1 6 | x + 2 y + 3 z |

V = 14 ⇒ 1 6 | x + 2 y + 3 z | = 14

⇒ | x + 2 y + 3 z | = 84

Então, por enquanto temos o sistema de equações:

x - 2 y + z = - 28

| x + 2 y + 3 z | = 84

Passo 2

Agora vamos fazer uso do fato de que O D → ,   O A → ∧ O B → , O A → ∧ O C → são l.d. Para isso, temos, primeiramente, que calcular os produtos vetoriais:

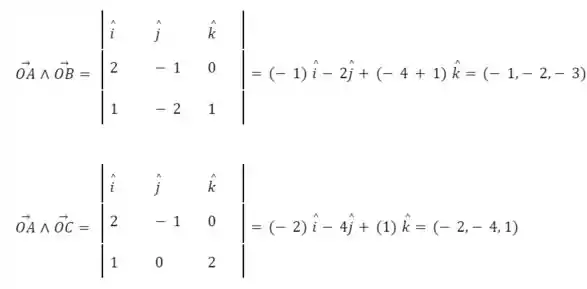
Agora podemos calcular o determinante dos três vetores, igualar a zero, e ver que condições obtemos

⇒ 4 z + y - 4 z - 2 x + 6 y - 12 x = 0

⇒ 7 y - 1 4 x = 0 ⇒ y - 2 x = 0 ⇒ y = 2 x

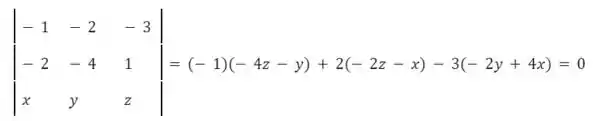
Passo 3

Nos passos anteriores, obtivemos as condições:

y = 2 x

x - 2 y + z = - 28

| x + 2 y + 3 z | = 84

Substituindo a primeira equação na segunda, obtemos

x - 2 y + z = - 28 ⇒ x - 4 x + z = - 28

⇒ - 3 x + z = - 28 ⇒ z = - 28 + 3 x

Vamos substituir esse resultado junto com y = 2 x na terceira equação:

| x + 2 y + 3 z | = 84 ⇒ | x + 4 x - 84 + 9 x | = 84

⇒ | 14 x - 84 | = 84

A equação acima pode ser satisfeita tanto por x = 0 quanto por x = 12 pois

x = 0 ⇒ | 14 x - 84 | = | - 84 | = 84

x = 12 ⇒ | 168 - 84 | = | 84 | = 84

Vamos substituir x = 0 em

y = 2 x = 0

z = - 28 + 3 x = - 28

e x = 12 em

y = 2 x = 24

z = - 28 + 3 x = 8

Então, podemos ter

O D →   =   ( 0,0 , - 28 )

ou

O D →   =   ( 12,24,8 )

Resposta

O D →   =   ( 0,0 , - 28 )

ou

O D →   =   ( 12,24,8 )

Exercícios de Livros Relacionados

Dados os pontos A 2,1 , 1 ,B - 1,0 , 1 eC ( 3,2 , - 2 ) , determinar o ponto D do eixo O z para que o volume do paralelepípedo determinado por A B → ,A C → e A D → seja 25u . v .
Determinar m e n para que se tenha:b) (m , n , 2) xx (4 , - 1,3) = ( 8 , - 1 , - 11 )
Sendo u → = 3 ,v → = 4e120 ° o ângulo entre os vetores u →ev → , calcular:c) o volume do paralelepípedo determinado por u → × v → ,u → e v → .
Sendo |vec u| = 3 , |vec v| = 4 e 120 ° o ângulo entre os vetores vec u e vec v , calcular:|vec u + vec v|
Determinar m e n para que se tenha:(m , n , 2) * (4 , - 1,3) = - 2