Considere o plano .
c) Determine as coordenadas dos vetores no sistema .
Passo 1
Para esta alternativa, precisamos lembrar qual é a definição de uma mudança de coordenadas. Ela é dada da seguinte forma:
Em que , uma matriz com os vetores de base como coluna, ou seja, na definição os vetores de base estarão nas linhas! Vamos fazer esta conta para a base canônica!
Passo 2
Precisamos fazer o produto matricial para cada vetor da base individualmente, temos que:
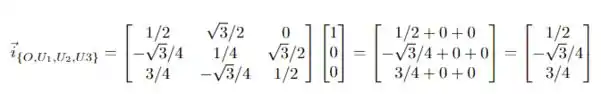
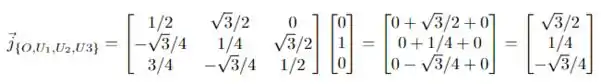
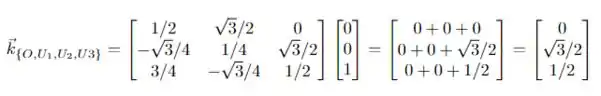
A questão foi isso! Te vejo na próxima! Tchauzinho!
Resposta
Ao longo dos passos