Enunciado
Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 5.4 - Ex. 2b
Encontre o ponto , se as coordenadas de em relação ao sistema de coordenadas , , são:
a) , em que
Passo 1
A ideia desta alternativa é a mesma da anterior, só que agora temos uma dimensão a mais! Bora repetir o processo, beleza?
Passo 2
Nós temos então que
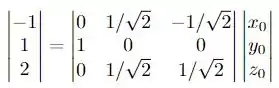
Fazendo o produto matricial temos que
Isso nos dá um sistema de equações lineares que podemos resolver, bora fazer isso!
Passo 3
O sistema é tal que temos as equações:
também temos que
e, por último:
A equação (2) nos diz diretamente que , portanto, vamos resolver o sistema para as outras duas equações, belezinha?
Passo 4
Da equação (1) temos que
e, portanto, a equação (3) nos dá:
e, portanto, com a equação (4), temos:
Portanto, temos o ponto . A questão é isso, te vejo na próxima!
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 5-8, use a equação da reta dada para encontrar um ponto na reta e um vetor paralelo à reta.8. x = 1 - t 0 , - 5, 1
Nos Exercícios 9-12, encontre as equações vetoriais e paramétricas do plano contendo o ponto e paralelo aos vetores.11. Ponto: - 1 , 1 , 4 ; vetores: v 1 = 6 , - 1 ,0 e v 2 = - 1 ,3 ,1
Nos Exercícios 9-12, encontre as equações vetoriais e paramétricas do plano contendo o ponto e paralelo aos vetores.10. Ponto: 0 , 6 , - 2 ; vetores: v 1 = 0 , 9 ,- 1 e v 2 = 0 ,- 3 ,0
Nos Exercícios 13-14, encontre as equações vetoriais e paramétricas da reta em R 2 que passa pela origem e é ortogonal a v .13. v = - 2,3
Nos Exercícios 13-14, encontre as equações vetoriais e paramétricas da reta em R 2 que passa pela origem e é ortogonal a v .16. v = 3 , 1 , - 6