Enunciado
Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 5.3 - Ex. 6
Considere as retas e em . Encontre a equação geral do plano que contém estas duas retas e ache um subconjunto com o maior número possível de vetores ortonormais neste plano.
Passo 1
Oiiie, tudo certinho?
Para resolver esta questão vamos nos lembrar a definição de ortogonalidade mais simples que pode ser utilizada neste problema, ou seja:
E também é necessário que e , para que eles sejam normalizados. A definição de norma é dada por:
Ou seja, nossos vetores de base devem obedecer às condições dadas acima, bora lá!
Passo 2
Vamos primeiro analisar ambas as equações da reta, comparando elas com o formato:
em que é um ponto pelo qual passa a reta, e é o vetor diretor da reta. Portanto, podemos identificar que da reta , temos:
e para a reta , temos que:
A primeira coisa que podemos tentar para encontrar a equação do nosso plano, é calcular o produto vetorial entre e , vamos tentar isso!
Passo 3
O produto vetorial toma a forma:
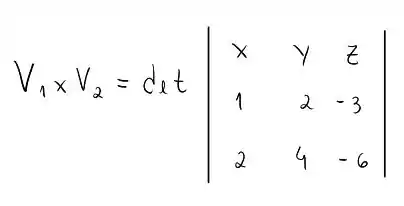
Você pode calcular o determinante desta matriz e verificar o resultado. Se ele dá zero, temos que os vetores são paralelos, então precisamos encontrar outro vetor para calcular nossa equação do plano, podemos fazer isso usando os pontos que passam pelas retas, bora lá!
Passo 4
O vetor que podemos construir é da forma:
e fazendo agora o produto vetorial:
Este resultado nos indica um vetor que é normal ao plano que contém os dois vetores, portanto, a equação geral do plano, toma a forma:
Passo 5
Nós temos 3 parâmetros livres e apenas uma equação, portanto, vamos escolher dois parâmetros quaisquer como e . E escrever o seguinte:
de forma que:
Esta expansão pode ser expandida em termos dos parâmetros da seguinte maneira:
De forma que nossa base pode ser identificada como e , que são L.I. Agora precisamos verificar a sua ortogonalidade e se são normalizados, belezinha?
Passo 6
Para verificar se são normalizados vamos utilizar a definição (1), tal que:
Eles não são ortogonais, portanto é preciso construir uma base ortogonal. Para isso vou introduzir a definição:
que é a projeção ortogonal de um vetor qualquer em um vetor não nulo , e portanto, podemos formar uma base ortogonal encontrando um segundo vetor tal que se:
temos que:
Vamos encontrar então a nossa base, bora bora!
Passo 7
Temos que:
Nós já calculamos . E podemos usar a definição (2) para obter:
e portanto, temos:
Portanto, nossa base é tal que . Vamos normalizá-la, e o problema acabou!
Passo 8
Um vetor normalizado pode ser obtido fazendo:
Portanto, temos que:
e usando a definição (2) para calcular:
e portanto, temos:
Aí está nossa base ortonormal, te vejo na próxima! Tchauzinho!