Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 4.Exercícios Propostos - Ex. 27

Dados os vetores u →   =   ( 2,2 , 4 ) e v →   =   ( 1,1 , 0 ) , determine uma base ortonormal positiva tal que seu primeiro vetor seja paralelo a u → e seu segundo vetor seja uma combinação linear de u → e v → . Determine, na base achada, as coordenadas de x →   = ( 1,0 , 0 ) .

Passo 1

Pessoal, vamos chamar o primeiro vetor da base de A → . Como ele deve ser paralelo a u →   =   ( 2,2 , 4 ) , então

A → =   α ( 2,2 , 4 )

Como A → deve ser unitário, então

| A → | = α 2 ( 4 + 4 + 16 ) = 1 ⇒ α 24 = 1 ⇒ α = 1 24 = 1 2 6

⇒ A → =   1 2 6 ( 2,2 , 4 ) = 1 6 ( 1,1 , 2 )

Passo 2

Agora, vamos obter o segundo vetor B → , que deve ser combinação linear de u →   =   ( 2,2 , 4 ) e v →   =   ( 1,1 , 0 ) :

B → = β   ( 2,2 , 4 ) + γ   ( 1,1 , 0 ) = ( 2 β + γ , 2 β + γ , 4 β )

O terceiro vetor terá a forma C → = ( a , b , c ) . Como a base é ortonormal positiva, então vale a relação entre o produto interno do primeiro vetor com o segundo:

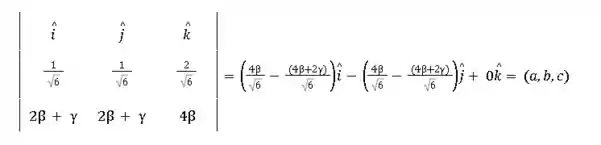
a   = 4 β 6 - ( 4 β + 2 γ ) 6   = -   2 γ 6 ; b   = +   2 γ 6 ⇒   a   =   - b e c = 0

Já podemos determinar o terceiro vetor com essas informações (   a   =   - b   e   c = 0 ) e usando a unitariedade do vetor:

| C → | = 1 ⇒ a 2 + b 2 + c 2 = 1 ⇒ a 2 + a 2 = 1 ⇒ 2 a = 1 ⇒ a = 1 2

⇒ b = - a = - 1 2

⇒ C → = 1 2 ( 1 , - 1,0 )

Além disso, temos

a   = -   2 γ 6 ⇒ γ = - 6 a 2 = - 6 2 ⋅ 1 2 = - 3 2

⇒ γ = - 3 2

Passo 3

Ok, galera! Já temos os vetores A → e C → , então só falta determinar

B → = ( 2 β + γ , 2 β + γ , 4 β )

Já sabemos também que γ = - 3 2 , então para encontrar β , vamos usar a condição de unitariedade:

| B → | = 1 ⇒ ( 2 β + γ ) 2 + ( 2 β + γ ) 2 + 16 β 2 = 1

⇒ 2 ( 4 β 2 + 4 γ β + γ 2 ) + 16 β 2 = 1

⇒ 24 β 2 + 8 γ β + 2 γ 2 = 1 ⇒ 24 β 2 + 8 γ β + 2 γ 2 = 1

⇒ 24 β 2 + 8 γ β + 2 γ 2 - 1 = 0

Substituindo γ = - 3 2 , obtemos

24 β 2 - 4 β 3 + 1 2 = 0 ⇒ β = 4 3 ± 48 - 48 2 ⋅ 24 = 3 12

Logo,

B → = ( 2 β + γ , 2 β + γ , 4 β ) = ( 3 6 - 3 2 , 3 6 - 3 2 , 3 3 ) = ( 3 - 3 3 6 , 3 - 3 3 6 , 3 3 )

B → = ( - 3 3 , - 3 3 , 3 3 ) = 1 3 ( - 1 , - 1,1 ) .

Passo 4

Calma, estamos quase lá. Agora só precisamos escrever x →   = ( 1,0 , 0 ) como uma combinação linear dos vetores da base:

x →   = x A → + y B → + z C → ⇒ ( 1,0 , 0 ) = x 6 ( 1,1 , 2 ) + y 3 ( - 1 , - 1,1 ) + z 2 ( 1 , - 1,0 )

⇒ ( 1,0 , 0 ) = 1 6 ( x - 2 y + 3 z , x - 2 y - 3 z , 2 x + 2 y )

⇒ x - 2 y + 3 z = 6

x - 2 y - 3 z = 0

2 x + 2 y = 0

Somando a primeira e a segunda equações, obtemos

2 x - 2 2 y = 6

Agora, subtraímos esse resultado da última equação:

2 x + 2 y - ( 2 x - 2 2 y ) = - 6

⇒ 3 2 y = - 6 ⇒ y = - 6 3 2 = - 3 3 = - 1 3

⇒ y = - 1 3

A terceira equação então se torna

2 x + 2 y = 0 ⇒ x = - 2 y 2 = - 2 2 - 3 3 = 2 ⋅ 3 2 ⋅ 3   = 6 6   = 1 6

Agora, substituímos os dois últimos resultados na primeira equação

x - 2 y + 3 z = 6 ⇒ 3 z = - x + 2 y + 6

⇒ 3 z = - 1 6 + 2 - 1 3 + 6 ⇒ 3 z   =   ( - 1 - 2 + 6 ) 6   = 3 2 ⋅ 3

z   =   3 3 2 ⋅ 3 =   1 2

Portanto, o vetor x →   = ( 1,0 , 0 ) pode ser escrito como

x →   = x A → + y B → + z C → = 1 6 A → - 1 3 B → + 1 2 C → = ( 1 6 , - 1 3 , 1 2 ) B

Resposta

A → = 1 6 ( 1,1 , 2 )

B → = 1 3 ( - 1 , - 1,1 )

C → = 1 2 ( 1 , - 1,0 )

x →   = ( 1 6 , - 1 3 , 1 2 ) B

Exercícios de Livros Relacionados

Com base na Figura 3.14, calculare) |vec B D xx vec A C|
Com base na Figura 3.14, calcularf) |vec B D xx vec C D|
Sendo |vec u| = 2 sqrt(2) , |vec v| = 4 e 45 ° o ângulo entre vec u e vec v , calcularb) |(2)/(5) vec u xx (1)/(2) vec v|
Determine vec u . vec v , sabendo que |vec u xx vec v| = 12 , |vec u| = 13 e vec v é unitário.
Dados os vetores u → = ( 1 ,1 ,0 ) e v → = ( - 1 ,1 ,2 ) , determinar:a) um vetor unitário simultaneamente ortogonal a u → e v → ;b) um vetor de módulo 5 simultaneamente ortogonal a u → e v → .