Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 5.Problemas - Ex. 1

Dado um paralelogramo ABCD, escolha um sistema de coordenadas adequado e mostre que A B - 2 + B C - 2 + C D - 2 + D A - 2 = A C - 2 + B D - 2 (a soma dos quadrados dos lados de um paralelogramo é igual à soma dos quadrados das suas diagonais).

Passo 1

Fala aí pessoal tudo blz?

Nessa questão ele pede para mostrarmos que a soma dos quadrados dos lados de um paralelogramo é igual a soma dos quadrados das diagonais, representado por,

A B - 2 + B C - 2 + C D - 2 + D A - 2 = A C - 2 + B D - 2

Pode ficar calminho que você vai entender legal, só confia.

Passo 2

Sabendo que,

A B - 2 + B C - 2 + C D - 2 + D A - 2 = A C - 2 + B D - 2 , temos

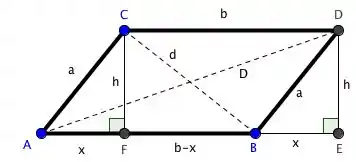
Aplicando Pitágoras nos triângulos, temos

A C F → a 2 = h 2 + x 2   ( I )

C F B → d 2 = b - x 2 + h 2 → d 2 = b 2 - 2 b x + x 2 + h 2   ( I I )

A D E → D 2 = h 2 + b 2 + 2 b x + x 2   ( I I I )

Somando ( I I ) com ( I I I ) , temos

D 2 + d 2 = b 2 - 2 b x + x 2 + h 2 + h 2 + b + 2 b x + x 2

D 2 + d 2 = 2 b 2 + 2 ( x 2 + h 2 )

Espero ter ajudado, e até a próxima.

Resposta

D 2 + d 2 = 2 b 2 + 2 ( x 2 + h 2 )

Exercícios de Livros Relacionados

Para cada uma das equações abaixo, descreva o conjunto dos pontos (x, y) cujas coordenadas satisfazem essa equação: y 2 - 6 y + 9 = 0
Para cada uma das equações abaixo, descreva o conjunto dos pontos (x, y) cujas coordenadas satisfazem essa equação: ( x 2 - 7 x + 10 ) ( y 2 - 7 x + 6 ) = 0
Para cada uma das equações abaixo, descreva o conjunto dos pontos (x, y) cujas coordenadas satisfazem essa equação: x 2 - 5 x + 6 = 0
Para cada uma das equações abaixo, descreva o conjunto dos pontos (x, y) cujas coordenadas satisfazem essa equação: x 2 + y 2 + 1 = 0
Em cada um dos casos abaixo, esboce o conjunto dos pontos cujas coordenadas x, y cumprem as condições especificadas: xy